การเลือกแบบจำลอง

ปัญหาหลักในการออกแบบอัลกอริทึมการเรียนรู้ก็คือการเลือก hypothesis space $H$ เราเรียกปัญหานี้ว่าปัญหา การเลือกแบบจำลอง (model selection) หาก $H$ ของเรามีขนาดใหญ่มาก เราก็อาจคาดหวังได้ว่า $H$ จะครอบคลุม Bayes hypothesis อย่างไรก็ดี จากการวิเคราะห์การเรียนรู้แบบ Agnostic PAC ก็จะเห็นว่าเมื่อ $H$ มีขนาดใหญ่ ขอบเขตของ generalization error ที่ได้จากการเรียนรู้ก็ยิ่งมากตามไปด้วย นั่นคือ hypothesis ที่ได้จากการเรียนรู้อาจมี error ไม่ใกล้เคียงกับ Bayes error เท่าที่ต้องการก็ได้ ในหัวข้อนี้เราจะมาวิเคราะห์ trade-off นี้ในรูปของ estimation error และ approximation error

Estimation error และ Approximation error

สำหรับ hypothesis $h\in H$ ใด ๆ เราสามารถเขียนผลต่างระหว่าง $R(h)$ และ Bayes error $R^*$ แบบแยกองค์ประกอบได้เป็น

$R(h)-R^* = \left(R(h) - R(h^*)\right) + \left(R(h^*) - R^*\right)$

เมื่อ $h^*$ เป็น hypothesis ที่มี error น้อยที่สุดใน $H$

เราเรียก $R(h)-R(h^*)$ ว่า estimation error และเรียก $R(h^*)-R^*$ ว่า approximation error โดย estimation error นั้นทำการวัด error ของ $h$ เทียบกับ error ที่น้อยที่สุดที่สามารถสร้างได้จาก $H$ สังเกตว่าในการเรียนรู้แบบ Agnostic PAC นั้น เรามุ่งเป้าไปที่การลด estimation error นี้เป็นหลัก

สำหรับ approximation error นั้นเป็นตัวที่บอกเราว่า $H$ นั้นสามารถประมาณค่า Bayes error $R^*$ ได้มากแค่ไหน หากเราเลือก $H$ ที่มีความซับซ้อนสูงซึ่งทำให้ $H$ มีขนาดใหญ่ ก็มีแนวโน้มที่จะได้ค่า approximation error ที่น้อย ในขณะที่ estimation error นั้นจะสูงตามขนาดของ $H$ รูปด้านล่างแสดงตัวอย่าง estimation error และ approximation error โดยเส้นทึบแทน estimation error และเส้นประแทน approximation error เมื่อ $h_{Bayes}$ เป็น Bayes hypothesis

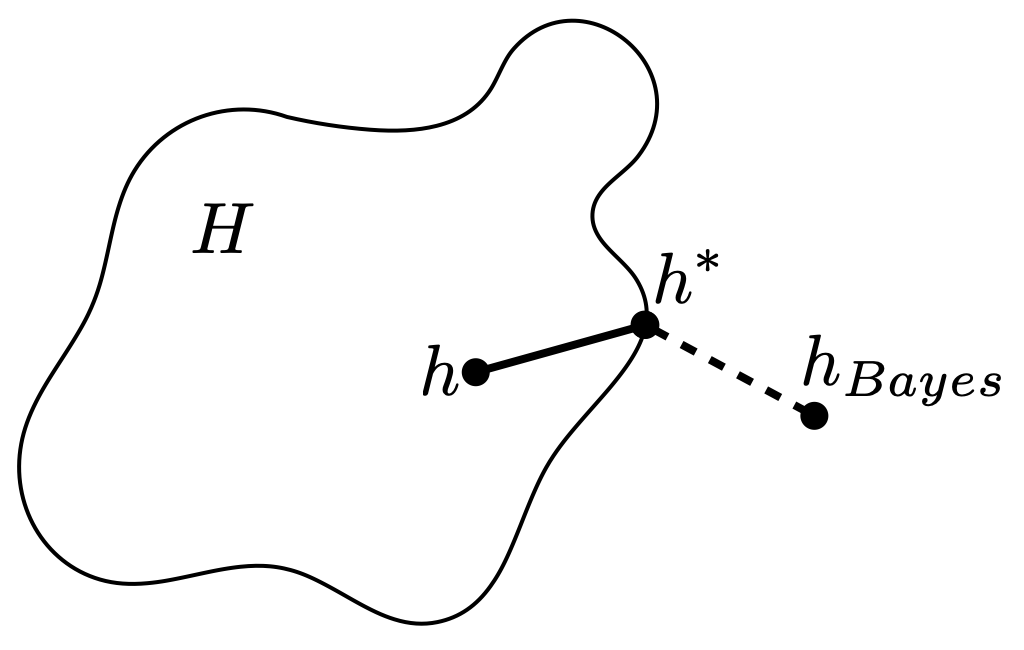
ในการเลือกแบบจำลองนั้น เราต้องเลือก hypothesis space $H$ ที่มี trade-off ระหว่าง estimation error และ approximation error นี้ในระดับที่เราพอใจ สังเกตว่าเราไม่สามารถประมาณค่า approximation error ได้เลย เพราะเราไม่รู้การกระจาย $D$ ของข้อมูล ในขณะที่ค่า estimation error ของ hypothesis ที่ได้จากอัลกอริทึมการเรียนรู้นั้น อาจจะประมาณด้วย generalization bound ได้ในบางสถานการณ์

ตัวอย่างหนึ่งของอัลกอริทึมที่สามารถประมาณค่า estimation error ได้ก็คือ empirical risk minimization (ERM) ที่เราได้ศึกษากันไปแล้วนั่นเอง ซึ่งสามารถประมาณค่า estimation error ในรูปของขนาดของ $H$ ได้ อย่างไรก็ดี ในทางปฏิบัตินั้นอัลกอริทึม ERM มักจะไม่ประสบความสำเร็จเนื่องจากขาดการพิจารณาความซับซ้อนของ hypothesis space $H$ ทำให้เมื่อ $H$ มีความซับซ้อนต่ำ approximation error ก็มีค่ามาก ในขณะที่เมื่อ $H$ มีความซับซ้อนสูงทำให้ขนาดของ $H$ มีค่ามาก ขอบเขตของ estimation error ก็จะกว้าง นอกจากนี้ ในหลายสถานการณ์ การหาผลลัพธ์ของ ERM ให้ได้นั้นก็เป็นปัญหายากในมุมของประสิทธิภาพของอัลกอริทึมอีกด้วย

Structural risk minimization

จากปัญหาการเลือกแบบจำลองที่แสดงในรูปของผลรวมระหว่าง estimation error และ approximation error จะเห็นว่าแบบจำลองหรือ hypothesis space ที่เหมาะสมนั้นควรจะมีความซับซ้อนมากพอที่จะทำให้ approximation error มีค่าน้อย แต่ต้องไม่ซับซ้อนมากเกินไปเพื่อให้ขอบเขตของ estimation error ไม่กว้างด้วย แนวทางหนึ่งในการหาแบบจำลองดังกล่าวคือการพิจารณา ลำดับของ hypothesis space ที่มีความซับซ้อนมากขึ้นเรื่อย ๆ ที่ละขั้น กล่าวคือ เราจะพิจารณา hypothesis space $H_1,H_2,H_3,\dots$ ที่

$H_i\subset H_{i+1}$

สำหรับ $i=1,2,3,\dots$ และพยายามหา hypothesis space $H_{i}$ ที่มี trade-off ระหว่าง estimation error กับ approximation error ดีที่สุด อย่างไรก็ดี เนื่องจากค่า error ดังกล่าว ไม่สามารถคำนวณได้ เราก็จะใช้ขอบเขตบนของผลรวมที่คำนวณได้เป็นตัวแทนในการตัดสินใจ

แนวคิดนี้นำมาสู่อัลกอริทึมที่ชื่อว่า structural risk minimization (SRM) ซึ่งจะทำการวนรอบพิจารณา hypothesis space $H_1,H_2,H_3,\dots$ ตามลำดับ และทำการหา hypothesis $h\in H_i$ ที่มีค่า

$\hat{R}(h)+\sqrt{\frac{\ln |H_i|}{2m}}+\sqrt{\frac{\ln i}{m}}$

น้อยที่สุด

เราอาจกล่าวได้ว่า ถ้า $h_{SRM}$ เป็น hypothesis ผลลัพธ์ของอัลกอริทึม SRM เราจะได้ว่า

$h_{SRM}=\arg\min_{i\geq 1,\\ h\in H_i} \hat{R}(h)+\sqrt{\frac{\ln |H_i|}{2m}}+\sqrt{\frac{\ln i}{m}}$

เราสามารถมองผลจากอัลกอริทึม SRM ว่าเป็นการหาค่า $i$ และ hypothesis space $H_i$ ที่เหมาะสมที่สุด และอัลกอริทึมจะทำการคืนค่าเป็นผลลัพธ์ของ ERM ใน $H_i$

ในการวิเคราะห์ เราสมมติให้ $H = \bigcup_iH_i$ และสำหรับ $h$ ใด ๆ ใน $H$ เราจะให้ $i(h)$ เป็น index ของ hypothesis space $H_{i(h)}$ ที่เล็กที่สุดที่ครอบคลุม $h$ กล่าวคือ $i(h)=\min_{H_i\ni h}i$ เราจะเริ่มจากการวิเคราะห์ความน่าจะเป็นที่ตลอดการทำงานของอัลกอริทึม SRM ของเรานี้ จะมี hypothesis $h$ อย่างน้อยหนึ่งตัวที่มี error $R(h)$ มากกว่า $C(h)=\hat{R}(h)+\sqrt{\frac{\ln |H_{i(h)}|}{2m}}+\sqrt{\frac{\ln i(h)}{m}}$ เกิน $\epsilon$ นั่นคือ

$\begin{split} \Pr&\left[\exists h\in H: R(h)-C(h)>\epsilon\right]\\ &=\Pr\left[\exists h\in H: R(h)>\hat{R}(h)+\sqrt{\frac{\ln |H_{i(h)}|}{2m}}+\sqrt{\frac{\ln i(h)}{m}}+\epsilon\right]\\ &\leq\Pr\left[\exists i\geq 1,\exists h\in H_i: R(h)>\hat{R}(h)+\sqrt{\frac{\ln |H_{i}|}{2m}}+\sqrt{\frac{\ln i}{m}}+\epsilon\right]\\ &=\Pr\left[\exists i\geq 1,\exists h\in H_i: R(h)-\hat{R}(h)>\sqrt{\frac{\ln |H_{i}|}{2m}}+\sqrt{\frac{\ln i}{m}}+\epsilon\right]\\ &\leq\sum_{i=1}^\infty\sum_{h\in H_i}\Pr\left[R(h)-\hat{R}(h)>\sqrt{\frac{\ln |H_{i}|}{2m}}+\sqrt{\frac{\ln i}{m}}+\epsilon\right]\\ &\leq\sum_{i=1}^\infty\sum_{h\in H_i}e^{-2m\left(\sqrt{\frac{\ln |H_{i}|}{2m}}+\sqrt{\frac{\ln i}{m}}+\epsilon\right)^2}\\ &\leq\sum_{i=1}^\infty|H_i|e^{-\ln|H_i|-2\ln i-2m\epsilon^2}\\ &=\sum_{i=1}^\infty |H_i|\cdot\frac{1}{|H_i|}\cdot\frac{1}{i^2}\cdot e^{-2m\epsilon^2}\\ &=e^{-2m\epsilon^2}\sum_{i=1}^\infty\frac{1}{i^2}\\ &=\frac{\pi^2}{6}e^{-2m\epsilon^2}\\ &\leq 2e^{-2m\epsilon^2} \end{split}$

คราวนี้ ถ้าให้ $h^*$ เป็น hypothesis ใน $H$ ที่มี error $R(h^*)$ น้อยที่สุด สังเกตว่า

$\begin{split} \Pr&\left[R(h_{SRM})-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right)>\epsilon\right]\\ &=\Pr\left[\left(R(h_{SRM})-C(h_{SRM})\right)+\left(C(h_{SRM})-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right)\right) > \epsilon\right]\\ \end{split}$

เนื่องจาก สำหรับตัวแปรสุ่ม $X_1$ และ $X_2$ ใด ๆ ถ้า $X_1+X_2>\epsilon$ แสดงว่าจะต้องมี $X_1$ หรือ $X_2$ ที่มีค่ามากกว่า $\epsilon/2$ ดังนั้นเราจึงได้ว่า

$\begin{split} \Pr&\left[R(h_{SRM})-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right)>\epsilon\right]\\ &\leq\Pr\left[R(h_{SRM})-C(h_{SRM})>\frac{\epsilon}{2}\right]\\ &\quad+\Pr\left[C(h_{SRM})-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right) > \frac{\epsilon}{2}\right]\\ &\leq 2e^{-m\epsilon^2/2} + \Pr\left[C(h^*)-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right) > \frac{\epsilon}{2}\right] \end{split}$

เนื่องจากอัลกอริทึมของเราเลือก $h_{SRM}$ ที่มีค่า $C(h_{SRM})$ น้อยที่สุด ดังนั้น $C(h_{SRM})\leq C(h^*)$ เมื่อแทนค่า $C(h^*)=\hat{R}(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}$ ก็จะได้เป็น

$\begin{split} \Pr&\left[R(h_{SRM})-\left(R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}}+\sqrt{\frac{\ln i(h^*)}{m}}\right)>\epsilon\right]\\ &\leq 2e^{-m\epsilon^2/2} + \Pr[\hat{R}(h^*)-R(h^*)>\frac{\epsilon}{2}]\\ &\leq 2e^{-m\epsilon^2/2}+e^{-m\epsilon^2/2}\\ &=3e^{-m\epsilon^2/2} \end{split}$

เมื่อกำหนดให้ $3e^{-m\epsilon^2/2}=\delta$ เราจะได้ว่า $\epsilon=\sqrt{\frac{2}{m}\ln\frac{3}{\delta}}$ ดังนั้นเราจึงได้ว่า ด้วยความน่าจะเป็นอย่างน้อย $1-\delta$

$R(h_{SRM})\leq R(h^*) + \sqrt{\frac{\ln |H_{i(h^*)}|}{2m}} + \sqrt{\frac{\ln i(h^*)}{m}} + \sqrt{\frac{2}{m}\ln\frac{3}{\delta}}$

สังเกตว่าขอบเขตที่ได้นี้ใกล้เคียงกับขอบเขตของ estimation error ที่วิเคราะห์ได้เมื่อกำหนดให้ใช้ hypothesis space $H_{i(h^*)}$ จุดแตกต่างที่สำคัญคือพจน์ $\sqrt{\frac{\ln i(h^*)}{m}}$ ซึ่งเป็นเหมือนราคาที่เพิ่มขึ้นมาเพื่อแลกกับการได้ hypothesis space $H_{i(h^*)}$ ที่เหมาะสม

Regularization

สังเกตว่าในอัลกอริทึม SRM นั้น เราสามารถมองได้ว่าอัลกอริทึมดังกล่าวทำการถ่วงน้ำหนักระหว่าง empirical error $\hat{R}(h)$ กับความซับซ้อนของ hypothesis space ซึ่งจะทำให้อัลกอริทึมอาจจะไม่ยอมเลือก hypothesis $h$ ใน space $H_i$ ที่ซับซ้อนมากถึงแม้ว่า empirical error $\hat{R}(h)$ จะน้อยมากก็ตาม เนื่องจาก $H_i$ มีความซับซ้อนมากเกินไป

มีอัลกอริทึมอีกกลุ่มหนึ่งที่ใช้แนวคิดในการถ่วงน้ำหนักด้วยความซับซ้อนของ hypothesis space เข้าไปในฟังก์ชันเป้าหมายเช่นเดียวกับ SRM โดยที่พจน์ที่ใช้นำเสนอความซับซ้อนของ hypothesis space นั้นเรียกว่า regularization term ซึ่งมักจะนิยามด้วยขนาดหรือ norm ของ hypothesis $h$ นั่นคือ ในอัลกอริทึมกลุ่มนี้ เราจะทำการหา hypothesis $h$ ที่มีค่า

$\hat{R}(h) + \lambda\|h\|$

น้อยที่สุด หรือกล่าวได้ว่า ถ้าให้ $h_{REG}$ แทน hypothesis ที่เป็นผลลัพธ์ของอัลกอริทึมแบบ regularization $h_{REG}$ จะมีค่าเป็น

$h_{REG}=\arg\min_{h\in H}\hat{R}(h)+\lambda\|h\|$

โดยเราจะเรียก $\lambda\geq 0$ ว่า regularization parameter ซึ่งใช้สำหรับกำหนดความสัมพันธ์แบบ trade-off ระหว่าง empirical error ของ hypothesis $h$ และความซับซ้อนของ $h$

สังเกตว่าอัลกอริทึมกลุ่มนี้สามารถใช้ในกรณีที่ hypothesis space $H$ หลักที่เราสนใจอาจไม่สามารถจัดเป็นลำดับของ hypothesis space ย่อย $H_1\subset H_2\subset \dots$ ก็ได้

Prev: การเรียนรู้แบบ Agnostic PAC

Next: Dichotomy

Computational-Learning-Theory

ทฤษฎีการเรียนรู้เชิงคำนวณ

การเลือกแบบจำลอง

Estimation error และ Approximation error

Structural risk minimization

Regularization