Dichotomy

ในการวิเคราะห์ sample complexity หรือ generalization bound ที่ผ่านมาทั้งหมดนั้น ขนาดของ hypothesis space $H$ ที่เราเลือกใช้มีบทบาทสำคัญอย่างมาก ตัวอย่างเช่นในการเรียนรู้แบบ agnostic-PAC เราสามารถสรุปได้ว่า สำหรับ hypothesis $h\in H$ ใด ๆ เมื่อเราทำการเรียนรู้จากตัวอย่างข้อมูลจำนวน $m$ ตัว เราจะได้ว่าด้วยความน่าจะเป็นไม่น้อยกว่า $1-\delta$

เราอาจเรียกพจน์ $\sqrt{\frac{1}{2m}(\ln|H|+\ln\frac{2}{\delta})}$ ว่า error bar ซึ่งทำหน้าที่บอกขอบเขตของความแตกต่างระหว่าง $R(h)$ ซึ่งเป็นค่า error จริงของ $h$ ที่เราไม่สามารถเข้าถึงได้ กับ $\hat{R}(h)$ ที่เราสามารถวัดได้จากตัวอย่างข้อมูล สังเกตว่า error bar นี้ขึ้นกับ $m$ และ $|H|$ ดังนั้นหากเราต้องการให้ error bar นี้มีค่าน้อย เราสามารถทำได้โดยการเพิ่มจำนวนข้อมูลในการเรียนรู้ (เพิ่มค่าของ $m$) หรือเลือก hypothesis space ที่มีขนาดเล็ก (ทำให้ $|H|$ มีค่าน้อย) ซึ่งก็จะมี trade-off ระหว่าง estimation error และ approximation error ดังที่เราได้ศึกษากันไปแล้ว อย่างไรก็ดี hypothesis space ที่ใช้จริงในทางปฏิบัติจำนวนมากมีขนาดเป็นอนันต์ ซึ่ง error bar นี้ไม่สามารถใช้กับ hypothesis space เหล่านี้ได้ จึงเป็นปัญหาตามมาว่า สำหรับ hypothesis space ที่มีขนาดเป็นอนันต์เหล่านี้ เราจะสามารถทำการเรียนรู้ตามกรอบของ PAC ได้อยู่หรือไม่

ในการวิเคราะห์ ปัญหาการเรียนรู้รูปสี่เหลี่ยมขนานแกน ทำให้เราเห็นว่าอย่างน้อยที่สุด ถึงแม้ว่าขนาดของ hypothesis space จะเป็นอนันต์ เราก็จะยังสามารถทำการเรียนรู้ได้ในบางกรณี เป้าหมายหลักของบทนี้คือ เราจะพยายามขยายผลของการวิเคราะห์ปัญหาการเรียนรู้ของเราให้รองรับการวิเคราะห์บน hypothesis space เหล่านี้ได้

ปัญหาของ Union bound

ในกรณีที่ hypothesis space $H$ มีขนาดจำกัดนั้น การวิเคราะห์ของเราหาขอบเขตความน่าจะเป็นที่คำตอบจากอัลกอริทึมใด ๆ จะเป็น hypothesis $h\in H$ ที่มี $|R(h)-\hat{R}(h)|>\epsilon$ โดยการจำกัดขอบเขตของความน่าจะเป็นที่จะมี hypothesis สักตัวเป็นไปตามเงื่อนไขนั้น กล่าวคือ ถ้าเราให้ $B_i$ แทนเหตุการณ์ที่ $|R(h_i)-\hat{R}(h_i)|>\epsilon$ ในการวิเคราะห์ของเรา เราพยายามจำกัดขอบเขตความน่าจะเป็นของเหตุการณ์

โดยเราใช้ union bound เป็นขอบเขตว่าความน่าจะเป็นของเหตุการณ์ดังกล่าวนี้จะมีค่า

เมื่อเราสามารถหาขอบเขตของความน่าจะเป็นของเหตุการณ์ย่อย $B_i$ แต่ละตัวได้เท่ากัน จึงเป็นที่มาที่ทำให้มีค่าของ $|H|$ ปรากฏใน generalization bound

อย่างไรก็ดี หากเหตุการณ์ $B_i$ ต่าง ๆ นั้นมีส่วนซ้อนทับกันมาก การใช้ union bound นี้จะทำให้ได้ขอบเขตที่ห่างจากความจริงเป็นอย่างมาก ตัวอย่างเช่น หาก $B_1$ และ $B_2$ เป็นเหตุการณ์ที่มีส่วนใน sample space ที่ซ้อนทับกันมากดังแสดงในรูปต่อไปนี้

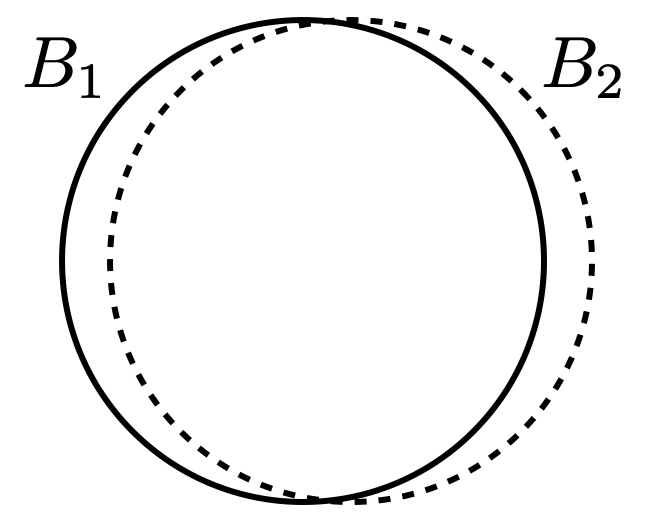
จะเห็นว่าความน่าจะเป็นของเหตุการณ์ $B_1\cup B_2$ นั้นแสดงได้ด้วยพื้นที่ดังรูปต่อไปนี้

ในขณะที่ขอบเขตของความน่าจะเป็นที่ได้จาก union bound นั้นแสดงได้ดังรูปต่อไปนี้ ซึ่งแตกต่างจากความจริงเป็นอย่างมาก

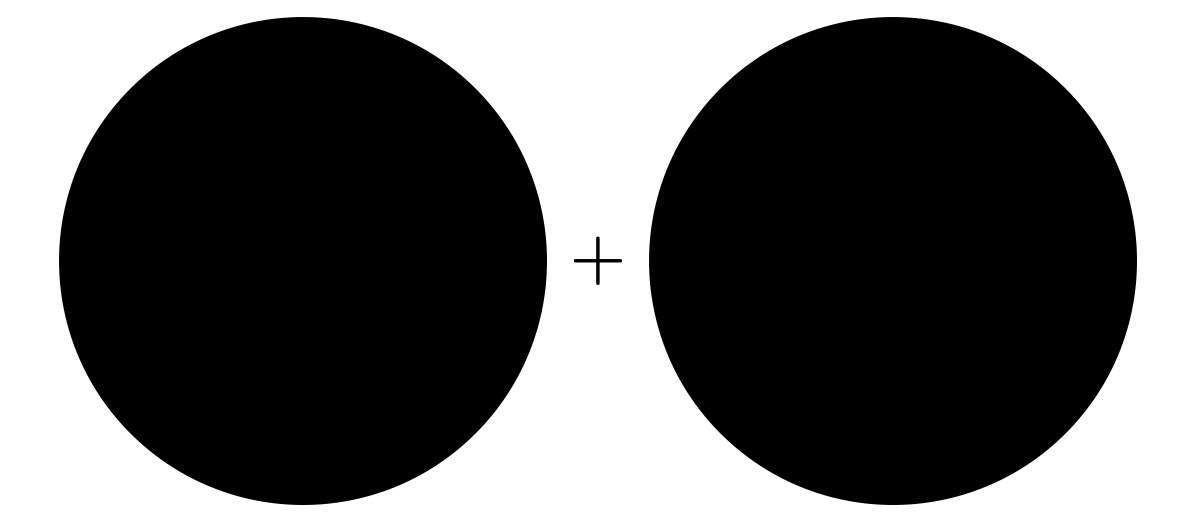
สำหรับ hypothesis space ที่มีขนาดเป็นอนันต์ เราจะพบว่ามี hypothesis จำนวนมากที่มีลักษณะใกล้เคียงกัน ตัวอย่างเช่นในปัญหาการเรียนรู้รูปสี่เหลี่ยมขนานแกน หากเราเลือกรูปสี่เหลี่ยม $h$ และทำการปรับขอบด้านบนของ $h$ ขึ้นด้วยค่าที่น้อยมาก ๆ เราจะได้รูปสี่เหลี่ยมใหม่ $h’$ ที่มีการตัดสินใจใกล้เคียงกับ $h$ มาก ซึ่งจะทำให้เหตุการณ์ $|R(h)-\hat{R}(h)|>\epsilon$ และ $|R(h’)-\hat{R}(h’)|>\epsilon$ เกิดขึ้นร่วมกันได้ง่าย หรือกล่าวได้ว่าเหตุการณ์ทั้งคู่มีส่วนซ้อนทับกันอยู่มาก ทำให้การใช้ union bound ซึ่งทำเหมือนว่าเหตุการณ์ทั้งคู่ไม่ซ้อนทับกันเลยนี้ได้ขอบเขตที่ห่างไกลความจริงเป็นอย่างมาก

ดังนั้นจะเห็นว่าในการวิเคราะห์ขอบเขตของ generalization bound สำหรับ hypothesis space ที่มีขนาดเป็นอนันต์เหล่านี้ เราจำเป็นต้องใช้เครื่องมืออย่างอื่นที่สามารถจำกัดขอบเขตได้ใกล้เคียงค่าจริงให้มากขึ้น

Hypothesis space ที่มองผ่านตัวอย่างข้อมูล

พิจารณา hypothesis space $H$ ใด ๆ ถึงแม้ว่าขนาดของ $H$ จะเป็นอนันต์ก็ตาม หากเรากำหนดเซตของตัวอย่างข้อมูล $\{x_1,\dots,x_m\}$ จะเห็นว่าจำนวนวิธีที่ hypothesis ใน $H$ จะสามารถจำแนกตัวอย่างข้อมูลกลุ่มนี้ออกเป็นสองคลาสนั้นจะมีจำนวนจำกัด ซึ่งมีค่าไม่เกิน $2^m$ แน่นอน สำหรับ hypothesis $h\in H$ เราจะเรียก $(h(x_1),\dots,h(x_m))$ ว่าเป็น dichotomy ของ $h$ บน $x_1,\dots,x_m$ และเราจะนิยามให้ dichotomy ของ $H$ เป็นดังนี้

นิยาม dichotomy ของ hypothesis space $H$ บนตัวแปร $x_1,\dots,x_m$ เขียนแทนด้วย $H(x_1,\dots,x_m)$ คือ

หรือกล่าวได้ว่า dichotomy ของ $H$ คือเซตของ dichotomy ที่เป็นไปได้ทั้งหมดที่จำแนกจาก hypothesis ใน $H$ สังเกตว่าหากเราพิจารณา input space ให้เหลือเพียง $\{x_1,\dots,x_m\}$ เราสามารถมอง $H(x_1,\dots,x_m)$ เป็น hypothesis space เช่นเดียวกับ $H$ ตัวอย่างเช่น ถ้าให้ $H$ เป็นเซตของ linear classifier บนระนาบสองมิติ และให้ตัวอย่างข้อมูล $x_1,x_2,x_3,x_4$ เป็นจุดสี่จุดบนระนาบดังรูปต่อไปนี้ รูปด้านซ้ายแสดงตัวอย่าง dichotomy หนึ่งของ $H(x_1,x_2,x_3,x_4)$ ที่จำแนกได้ด้วย hypothesis $h$ ที่แทนด้วยเส้นตรงในรูป ในขณะที่รูปด้านขวาแทนตัวอย่าง dichotomy ที่ไม่มีใน $H(x_1,x_2,x_3,x_4)$ (นั่นคือ ไม่สามารถจำแนกได้ด้วยเส้นตรงใด ๆ บนระนาบ)

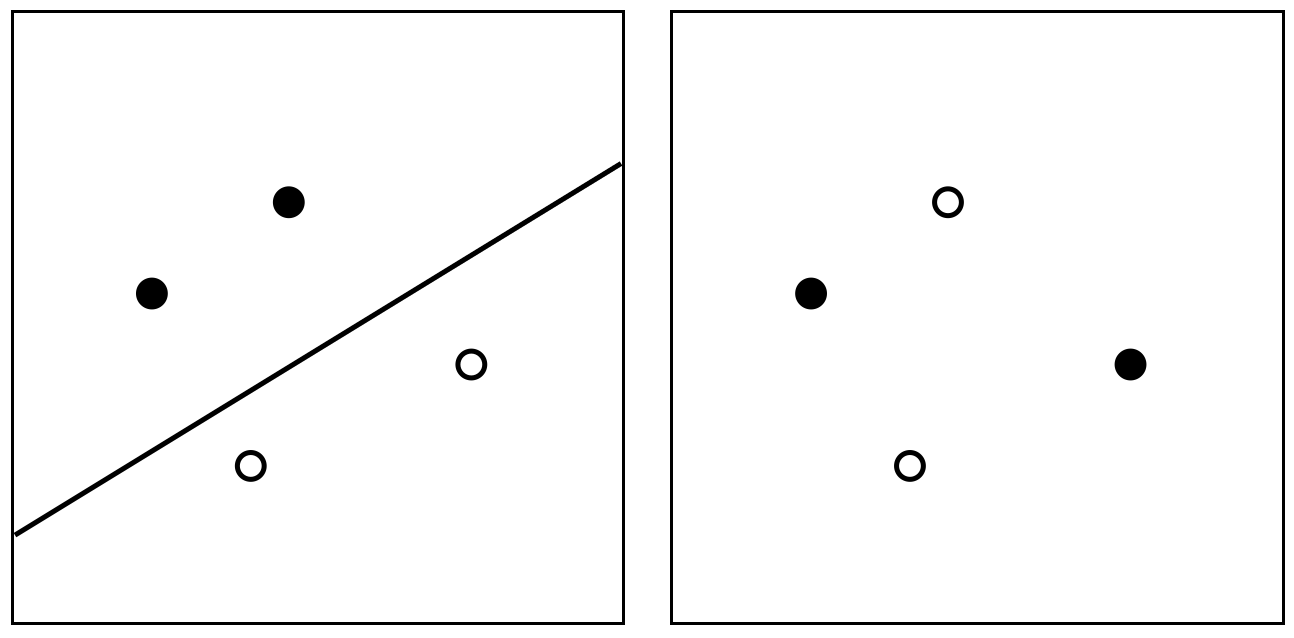
ถ้าเราสามารถสร้าง dichotomy จาก $H$ ได้ครบทั้ง $2^m$ แบบ เราจะกล่าวว่า $H$ shatter $\{x_1,\dots,x_m\}$ จากรูปด้านบน จะเห็นว่าเซตของ linear classifier บนระนาบนั้นไม่ shatter ตัวอย่างข้อมูลทั้งสี่จุดในรูป

Prev: การเลือกแบบจำลอง

Next: Growth Function