ปัญหาการเรียนรู้รูปสี่เหลี่ยมขนานแกน
ในหัวข้อนี้เราจะมาดูตัวอย่างปัญหาการเรียนรู้หนึ่งซึ่งมีอัลกอริทึมที่สามารถเรียนรู้ได้อย่างมีประสิทธิภาพตาม PAC-framework โดยในปัญหานี้ เราให้ $X$ เป็นเซตของจุดทั้งหมดในระนาบ นั่นคือ $X=\mathbb{R}^2$ และ concept class $C$ ของเราแทนเซตของรูปสี่เหลี่ยมผืนผ้าทั้งหมดที่มีด้านขนานกับแกนของระนาบ โดยสำหรับ รูปสี่เหลี่ยมของ concept $c$ ใด ๆ เราจะให้ $c(x)=1$ ถ้า $x$ เป็นจุดที่อยู่ภายในรูปสี่เหลี่ยมนั้น และ $c(x)=0$ ถ้า $x$ อยู่ภายนอก ปัญหาของเราคือต้องการหารูปสี่เหลี่ยมที่ใกล้เคียงกับ $c$ โดยเรียนรู้จากตัวอย่างข้อมูล รูปด้านล่างนี้แสดงตัวอย่างรูปสี่เหลี่ยม $r$ ที่เป็น concept เป้าหมาย และตัวอย่างข้อมูลโดยจุดดำแสดงตัวอย่างข้อมูลที่มี label เป็น 1 และจุดขาวเป็นข้อมูลที่มี label เป็น 0
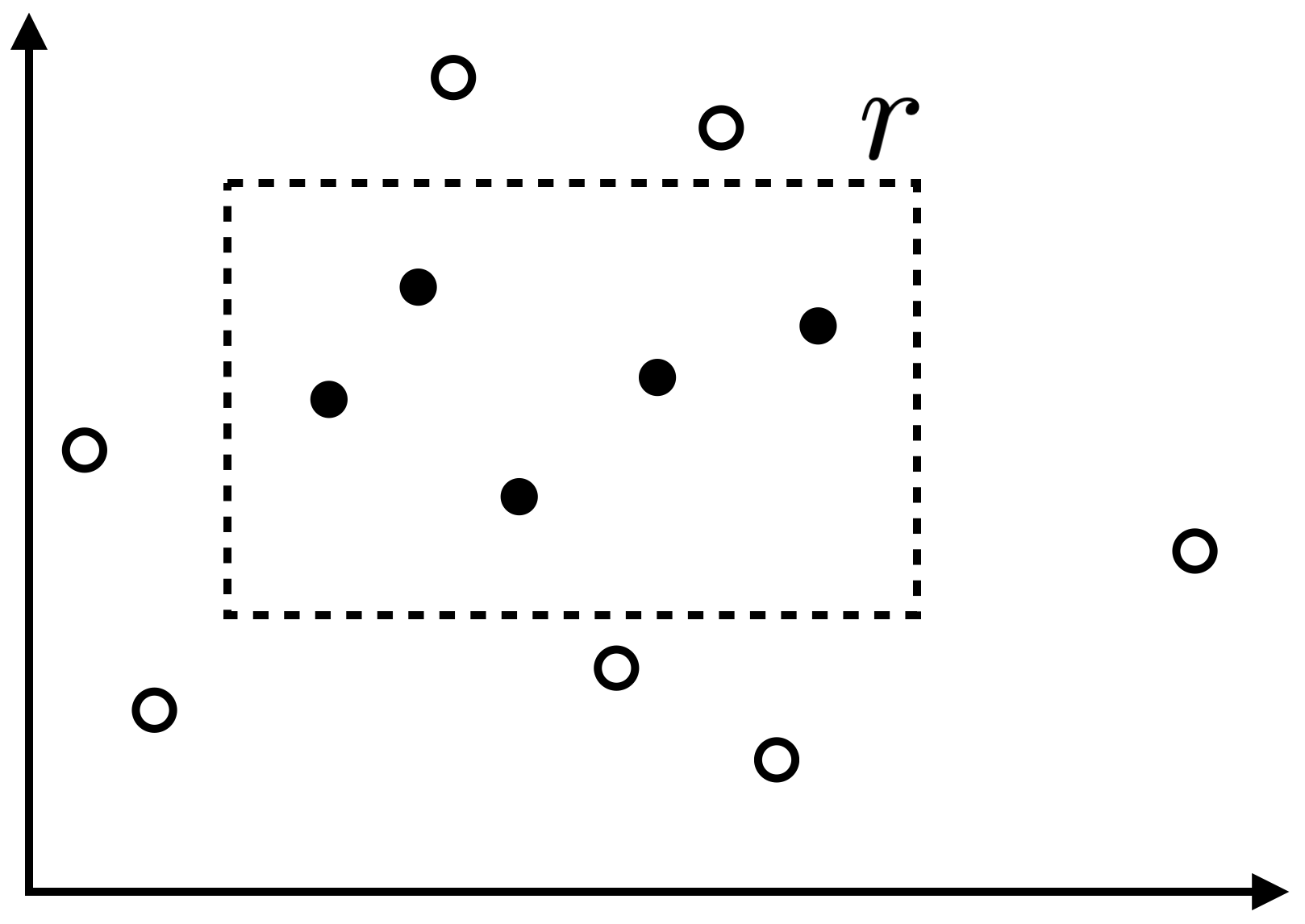
อัลกอริทึมการเรียนรู้
อัลกอริทึมหนึ่งที่สามารถเรียนรู้รูปสี่เหลี่ยม $r$ ได้ง่าย มีการทำงานดังนี้ เมื่อได้รับตัวอย่างข้อมูล อัลกอริทึมเราจะคืนคำตอบเป็นรูปสี่เหลี่ยมที่เล็กที่สุดที่ครอบคลุมตัวอย่างข้อมูล $x_i$ ทั้งหมดที่ $y_i=1$ ตัวอย่างผลของอัลกอริทึมคือรูปสี่เหลี่ยม $h$ ที่แสดงในรูปด้านล่างนี้
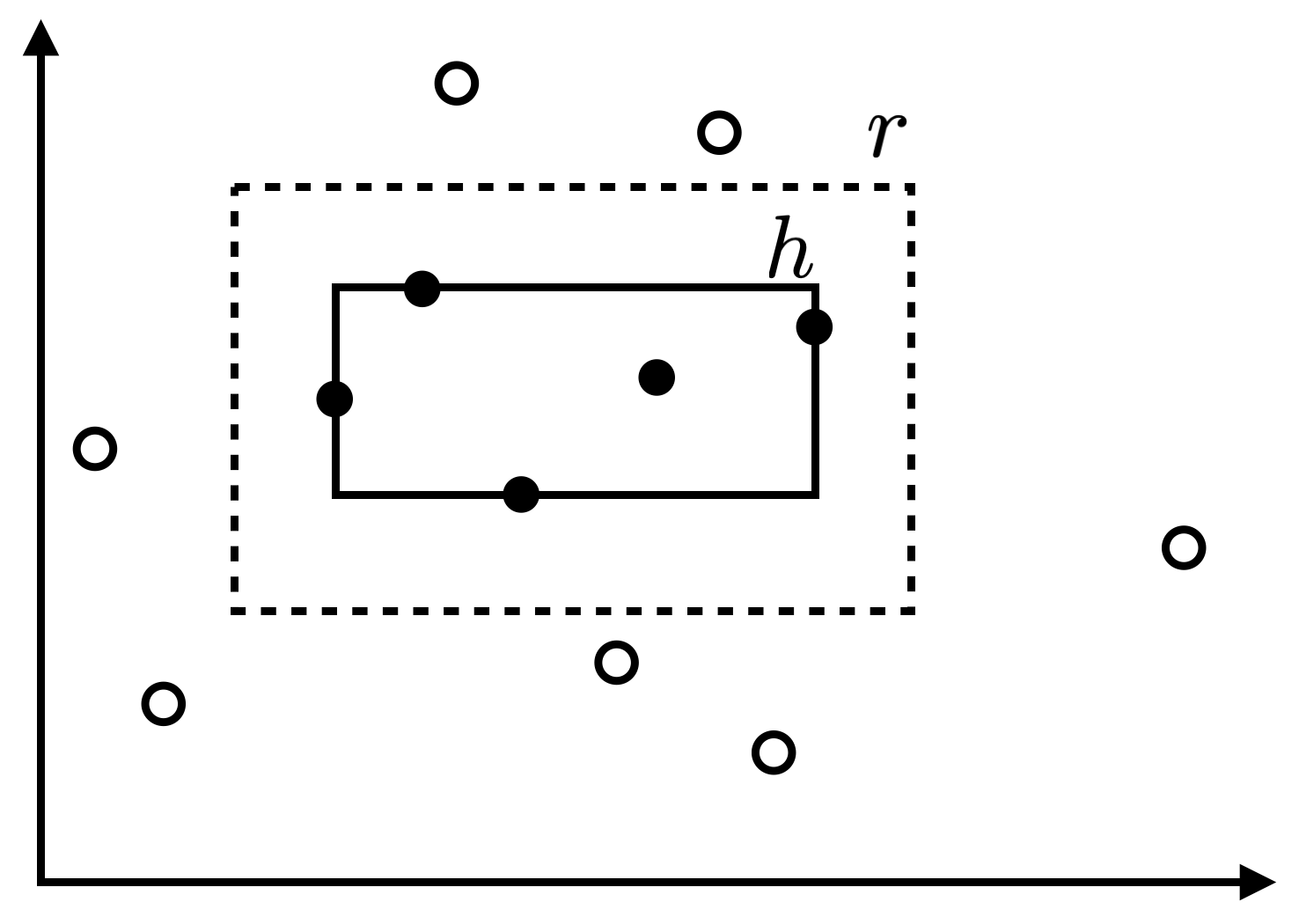
การวิเคราะห์ sample complexity
หากเรากำหนดค่า $\epsilon>0$ และต้องการวิเคราะห์ความน่าจะเป็นที่ $R(h)>\epsilon$ เราสามารถทำได้โดย สมมติให้ $t_1,t_2,t_3,t_4$ เป็นพื้นที่ที่ลากจากขอบด้านหนึ่งของรูปสี่เหลี่ยมเป้าหมาย $r$ เข้ามาด้านในให้มีความน่าจะเป็นที่จะสุ่มหยิบข้อมูลได้ภายในพื้นที่นั้นเท่ากับ $\epsilon/4$ พอดี (พื้นที่สีเทาในรูปด้านล่างแสดงตัวอย่างของพื้นที่ดังกล่าวที่ลากจากขอบด้านซ้ายของ $r$ เข้ามา)
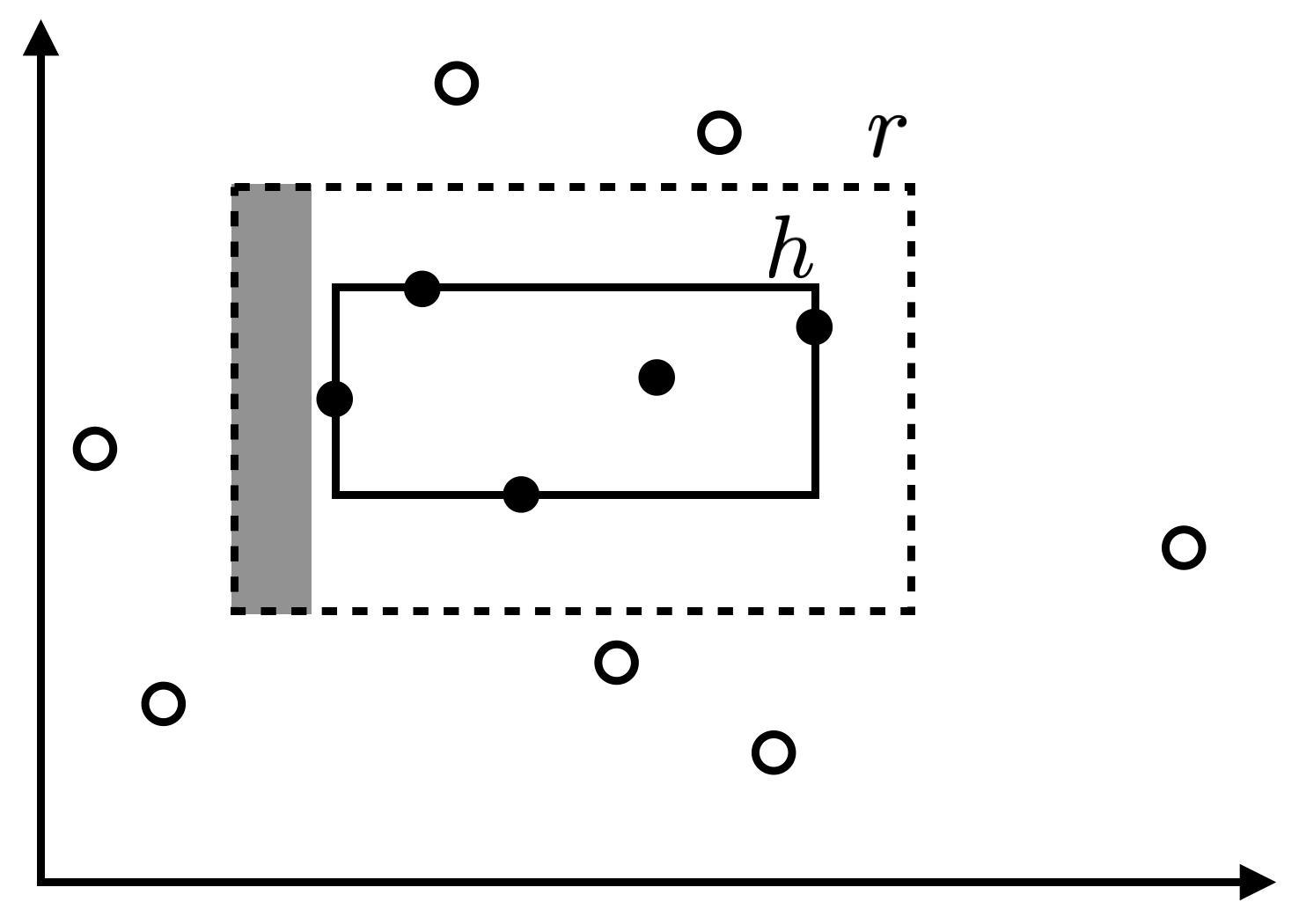
จาก union bound ซึ่งกล่าวว่า
เราจะได้ว่า
สังเกตว่าหากขอบของ $h$ เข้าไปแตะภายในพื้นที่ $t_i$ ทั้งสี่ด้าน แสดงว่าโอกาสที่เราจะสุ่มหยิบข้อมูล $x$ มาแล้วทำให้ $h(x)\neq r(x)$ ซึ่งก็คือโอกาสที่สุ่มหยิบ $x$ มาอยู่ภายในรูป $r$ แต่อยู่นอก $h$ นั้นต้องมีค่าไม่เกิน $\epsilon$ นั่นหมายความว่า ถ้า $R(h)>\epsilon$ แสดงว่าจะต้องมีอย่างน้อยด้านหนึ่งที่ขอบของรูปสี่เหลี่ยม $h$ นั้นไม่ได้เข้าไปแตะภายในพื้นที่ $t_i$ (เช่นด้านซ้ายในรูปด้านบน) เราอาจกล่าวได้ว่า ถ้า $R(h)>\epsilon$ แสดงว่าจะต้องมีพื้นที่ $t_i$ อย่างน้อยด้านหนึ่งที่ $t_i\cap h=\emptyset$ ดังนั้นเราได้ว่า
คราวนี้สังเกตว่าหากตัวอย่างข้อมูลของเรามีการสุ่มข้อมูล $x$ ที่อยู่ภายในพื้นที่ $t_i$ อย่างน้อยตัวหนึ่ง รูปสี่เหลี่ยม $h$ ของเราก็ต้องครอบคลุมข้อมูล $x$ ตัวนั้นด้วย แสดงว่าขอบของ $h$ ต้องเข้าไปแตะในพื้นที่ $t_i$ แน่นอน การที่ขอบของ $h$ ไม่ได้แตะเข้าไปในพื้นที่ $t_i$ แสดงว่าในตัวอย่างข้อมูลทั้ง $m$ ตัวของเรานั้น ไม่มีข้อมูลที่อยู่ในพื้นที่ $t_i$ เลยสักตัวเดียว เนื่องจากข้อมูลแต่ละตัวสุ่มหยิบมาแบบ i.i.d. โดยมีโอกาสตกอยู่ใน $t_i$ ด้วยความน่าจะเป็น $\epsilon/4$ แสดงว่าโอกาสที่ข้อมูลทั้ง $m$ ตัวหยิบมาไม่โดน $t_i$ เลยจะเท่ากับ $(1-\epsilon/4)^m$ ดังนั้นเราจึงได้ว่า
เนื่องจาก $1+x\leq e^x$ สำหรับ $x\in\mathbb{R}$ ใด ๆ
ถึงตรงนี้ หากเราต้องการให้ $\Pr[R(h)>\epsilon]$ มีค่าไม่เกิน $\delta$ เราสามารถทำได้โดยกำหนดให้ $4e^{-m\epsilon/4}\leq\delta$ ซึ่งจะได้เงื่อนไขว่า
โดยสรุป สำหรับค่า $\epsilon>0$ และ $\delta>0$ ใด ๆ หากเรามีตัวอย่างข้อมูลจำนวนอย่างน้อย $\frac{4}{\epsilon}\ln\frac{4}{\delta}$ ตัว อัลกอริทึมของเราจะให้รูปสี่เหลี่ยม $h$ ที่รับประกันได้ว่า $\Pr[R(h)>\epsilon]\leq\delta$ สังเกตว่าจำนวนตัวอย่างข้อมูลที่ต้องการนี้เป็น polynomial บน $1/\epsilon$ และ $1/\delta$ ดังนั้นอัลกอริทึมของเราเป็นอัลกอริทึมการเรียนรู้ที่มีประสิทธิภาพ โดยมี sample complexity เป็น $O(\frac{1}{\epsilon}\log\frac{1}{\delta})$
generalization error
เราสามารถนำเสนอข้อสรุปจากการวิเคราะห์อัลกอริทึมการเรียนรู้ของเราในอีกลักษณะหนึ่งได้ โดยถ้าเรากำหนดให้ $4e^{-m\epsilon/4}=\delta$ พอดี เราจะได้ว่า $\epsilon = \frac{4}{m}\ln\frac{4}{\delta}$ นั่นคือ สำหรับตัวอย่างข้อมูลจำนวน $m$ ตัว ด้วยความน่าจะเป็นอย่างน้อย $1-\delta$ อัลกอริทึมของเราจะให้ผลเป็น hypothesis $h$ ที่มี error