การเรียนรู้รูปสี่เหลี่ยมขนานแกนเมื่อมีการรบกวน

ในหัวข้อนี้เราจะมาศึกษาการเรียนรู้ในกรณีที่ตัวอย่างข้อมูลที่ได้รับมานั้นมีการรบกวนเกิดขึ้น โดยการรบกวนที่เราสนใจคือการรบกวน label ของตัวอย่างข้อมูล ซึ่งอาจจะทำให้ตัวอย่างข้อมูลที่ได้รับมาบางตัวมี label ไม่ถูกต้อง เราจะมาวิเคราะห์กันว่าในสถานการณ์เช่นนี้เราจะยังสามารถทำการเรียนรู้ตามกรอบ PAC ได้อยู่หรือไม่ และ generalization bound หรือ sample complexity ของการเรียนรู้จะเปลี่ยนไปมากน้อยเท่าไหร่

ปัญหาการเรียนรู้รูปสี่เหลี่ยมขนานแกนเมื่อมีการรบกวน

เราจะมาดูตัวอย่างใน ปัญหาการเรียนรู้รูปสี่เหลี่ยมขนานแกน ซึ่งเราเคยวิเคราะห์กันมาแล้วว่าในกรณีที่ตัวอย่างข้อมูลนั้นไม่มีการรบกวน เราสามารถเรียนรู้รูปสี่เหลี่ยมขนานแกนได้อย่างมีประสิทธิภาพ โดยอัลกอริทึมการเรียนรู้หนึ่งที่ใช้ได้ คือการตอบรูปสี่เหลี่ยมที่เล็กที่สุดที่ครอบคลุม positive example ทั้งหมด

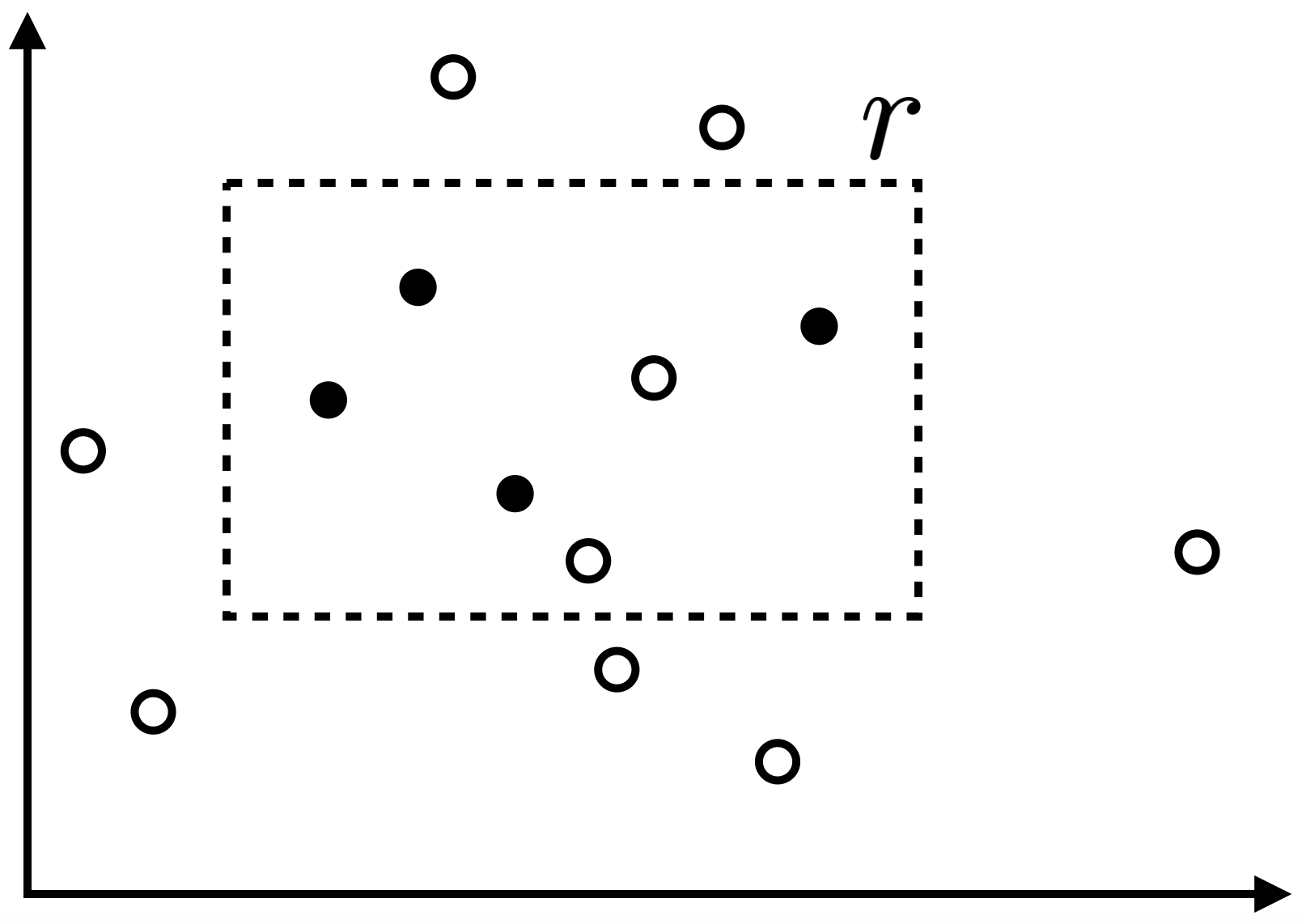
ในคราวนี้สมมติว่าตัวอย่างข้อมูลที่เราได้รับมานั้นอาจถูกรบกวนในลักษณะที่ สำหรับ negative example $(x,0)$ ใด ๆ การรบกวนจะไม่ส่งผลให้ข้อมูลเปลี่ยนแปลง แต่สำหรับ positive example $(x, 1)$ ใด ๆ นั้นจะถูกการรบกวนเปลี่ยนให้กลายเป็น negative example $(x,0)$ ด้วยความน่าจะเป็น $\eta$ โดย $0<\eta<\frac{1}{2}$ โดยที่เราไม่สามารถรู้ค่าที่แท้จริงของ $\eta$ ได้ แต่รู้ขอบเขตบน $\eta’$ ซึ่ง $\eta\leq\eta’<\frac{1}{2}$ รูปด้านล่างแสดงตัวอย่างของข้อมูลที่ถูกรบกวนที่เราได้รับมา เมื่อ $r$ เป็นรูปสี่เหลี่ยมเป้าหมาย โดยจุดทึบแทน positive example และจุดขาวแทน negative example

รูปสี่เหลี่ยมที่เล็กที่สุดที่ครอบคลุม positive example

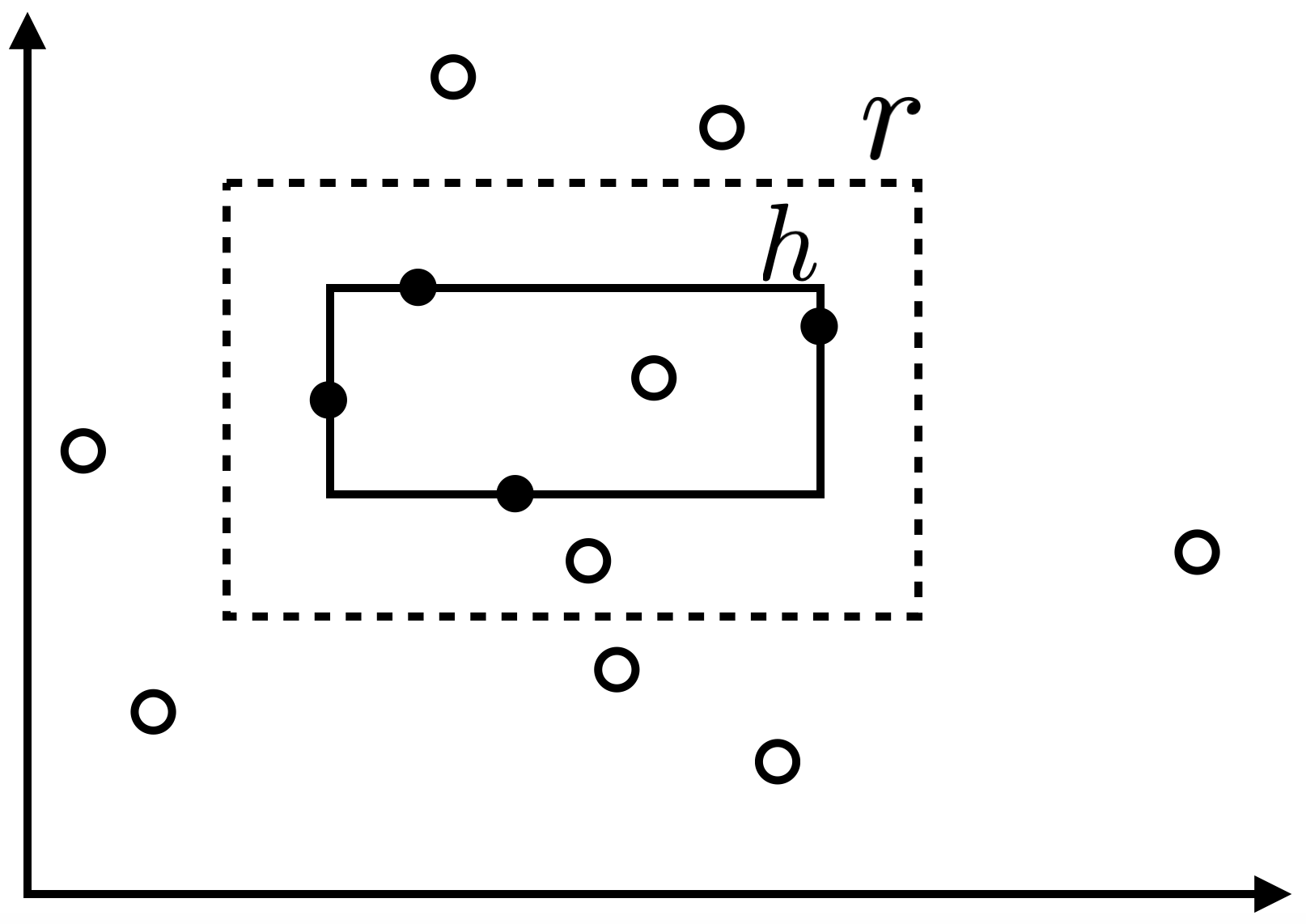
สังเกตว่าในกรณีนี้ เราไม่สามารถรับประกันได้ว่าจะหารูปสี่เหลี่ยมขนานแกนที่สามารถจำแนก positive example และ negative example ทั้งหมดออกจากกันได้เสมอ อย่างไรก็ดีเราจะแสดงให้เห็นว่าอัลกอริทึมการเรียนรู้เดิม ที่ทำการตอบรูปสี่เหลี่ยมที่เล็กที่สุดที่ครอบคลุม positive example ทั้งหมด (และอาจครอบคลุม negative example บางตัวด้วย) ยังสามารถทำการเรียนรู้ปัญหานี้ได้ ตัวอย่างเช่น หากตัวอย่างข้อมูลที่ได้รับมาเป็นดังรูปด้านบน อัลกอริทึมของเราจะตอบรูปสี่เหลี่ยม $h$ ดังรูปต่อไปนี้

เราจะทำการวิเคราะห์คุณสมบัติของ $h$ ด้วยวิธีการแบบเดิม สมมติให้ $R(h)>\epsilon$ และให้ $t_1,t_2,t_3,t_4$ เป็นพื้นที่ที่ลากจากขอบด้านหนึ่งของรูปสี่เหลี่ยมเป้าหมาย $r$ เข้ามาด้านในให้มีความน่าจะเป็นที่จะสุ่มหยิบข้อมูลได้ภายในพื้นที่นั้นเท่ากับ $\epsilon/4$ พอดี (พื้นที่สีเทาในรูปด้านล่างแสดงตัวอย่างของพื้นที่ดังกล่าวที่ลากจากขอบด้านล่างของ $r$ เข้ามา)

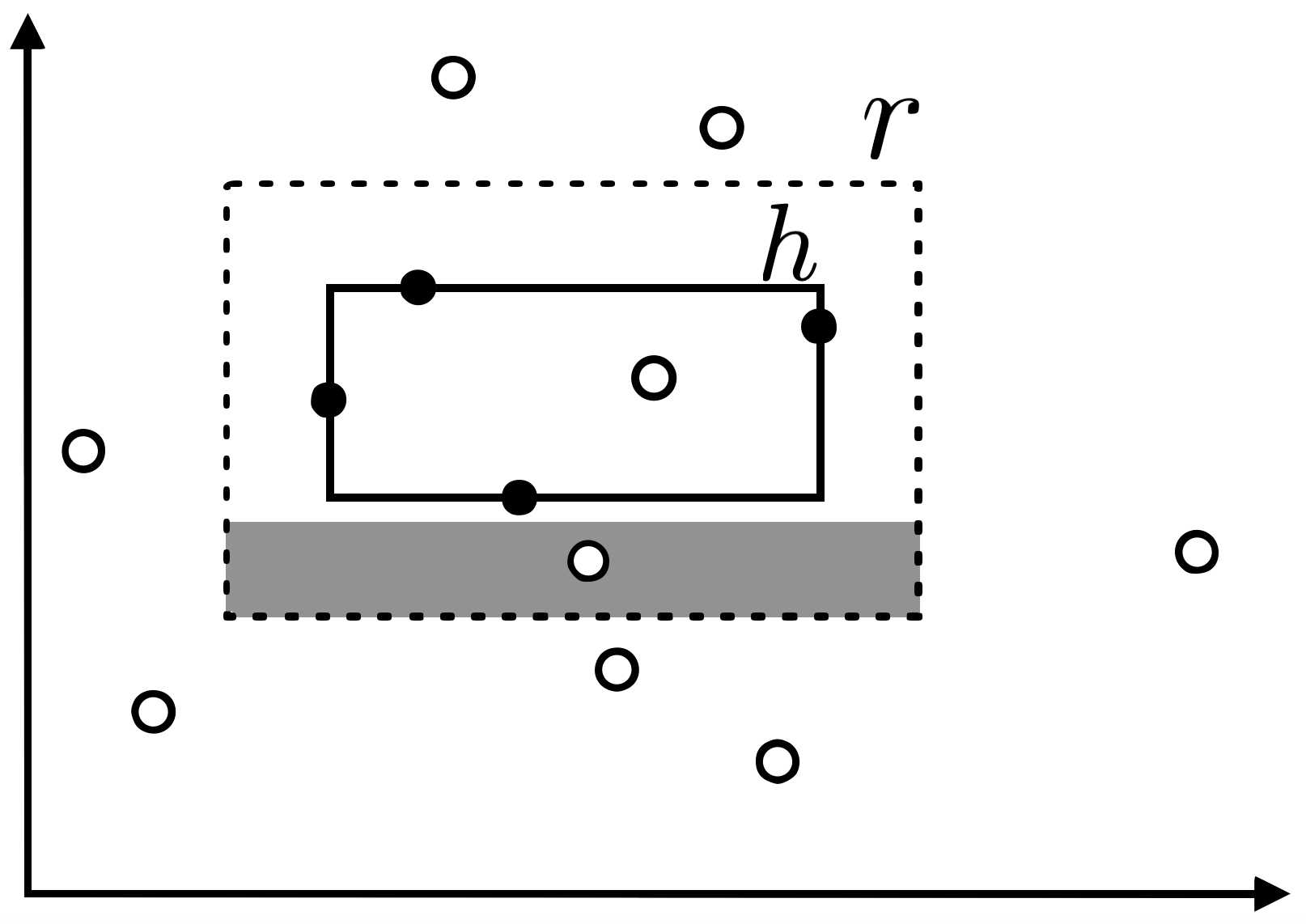
เราจะได้ว่า การที่ $R(h)>\epsilon$ แสดงว่าจะต้องมีขอบของ $h$ อย่างน้อยด้านหนึ่งที่ไม่แตะเข้าไปยังพื้นที่ $t_i$ ของด้านนั้น นั่นคือ

คราวนี้เมื่อพิจารณาที่พื้นที่ $t_i$ แต่ละด้าน การที่รูปสี่เหลี่ยม $h$ ที่เป็นคำตอบของอัลกอริทึมนั้นไม่ซ้อนทับกับ $t_i$ แสดงว่าในตัวอย่างข้อมูลของเราไม่มี positive example สักตัวที่ตกอยู่ในพื้นที่ $t_i$ เลย หากเราพิจารณาการสุ่มตัวอย่างข้อมูล $x$ แต่ละตัว สังเกตว่าในสถานการณ์นี้ การที่ตัวอย่างข้อมูล $x$ ของเราไม่ได้ปรากฏเป็น positive example ใน $t_i$ อาจไม่ใช่เพราะเราสุ่มได้ $x$ อยู่นอกพื้นที่ $t_i$ เพียงอย่างเดียว แต่อาจเกิดจากการสุ่มได้ $x$ ที่อยู่ในพื้นที่ $t_i$ แต่ถูกรบกวนจนกลายเป็น negative example ในพื้นที่ $t_i$ แทนก็ได้ (เช่น negative example ในพื้นที่สีเทาในรูปด้านบน) ดังนั้น สำหรับตัวอย่างข้อมูล $x$ แต่ละตัว เราสามารถหาความน่าจะเป็นที่ $x$ ไม่ได้ปรากฏเป็น positive example ในพื้นที่ $t_i$ แก่เราได้เป็น

ดังนั้น ความน่าจะเป็นที่ตัวอย่างข้อมูลทั้ง $m$ ตัวจะไม่ปรากฏเป็น positive example ในพื้นที่ $t_i$ เลยสักตัวเดียว จะมีค่าเป็น

ดังนั้น

ซึ่งถ้าเรากำหนดให้ $4e^{-m\epsilon(1-\eta’)/4}\leq\delta$ เราก็จะได้ sample complexity สำหรับการเรียนรู้ในสถานการณ์นี้ได้ว่า เราสามารถหารูปสี่เหลี่ยมขนานแกน $h$ ที่ $R(h)\leq\epsilon$ ด้วยความน่าจะเป็นไม่น้อยกว่า $1-\delta$ เมื่อมีจำนวนตัวอย่างข้อมูล $m$ ดังนี้

หรือสามารถวิเคราะห์ในรูปแบบของ generalization error ได้ว่า ด้วยความน่าจะเป็นไม่น้อยกว่า $1-\delta$

Prev: Decision Tree

Next: การเรียนรู้แบบ PAC เมื่อมีการรบกวน