Decision Tree
ในหัวข้อนี้เราจะมารู้จักการนำเสนอ boolean function อีกลักษณะหนึ่งที่เรียกว่า decision tree ซึ่งเป็นหนึ่งในแบบจำลองที่นิยมใช้ในปัญหาด้าน machine learning ในทางปฏิบัติจริง ๆ เราจะมาวิเคราะห์ความสามารถของ decision tree ในการ represent ฟังก์ชันทาง boolean และศึกษาประสิทธิภาพในการเรียนรู้แบบจำลอง decision tree นี้
ก่อนอื่น เราจะให้นิยาม decision tree อย่างเป็นทางการเสียก่อน สำหรับตัวแปร boolean $x_1,\dots,x_n$ ใด ๆ เราจะกล่าวว่า $T$ เป็น decision tree บน $x_1,\dots,x_n$ เมื่อ $T$ เป็น full binary tree (binary tree ที่ internal node ทั้งหมดมีจำนวน node ลูกเท่ากับ 2) โดยที่แต่ละ internal node จะถูก label ด้วยตัวแปร $x_i$ ตัวหนึ่ง และแต่ละ leaf node ถูก label ด้วย 0 หรือ 1
Decision tree ความสูง $k$ represent ได้ด้วย $k$-DNF
สำหรับ decision tree $T$ ใด ๆ $T$ จะทำหน้าที่ represent ฟังก์ชัน $f_T$ บน input ที่สามารถนิยามแบบ recursive ได้ดังนี้ ถ้า $T$ เป็น tree ที่มีเพียง node เดียว ซึ่งถูก label ด้วย $f_T$ จะเป็นฟังก์ชันที่คืนค่าเป็นค่าคงที่ $b$ เสมอไม่ว่าจะรับ input เป็นอะไรก็ตาม แต่หาก $T$ มี root ที่ถูก label ด้วยตัวแปร $x_i$ และมี $T_0$ และ $T_1$ เป็นต้นไม้ย่อยด้านซ้ายและขวาของ root ของ $T$ ตามลำดับ เราจะได้ว่า $f_T(a)$ จะมีค่าเท่ากับ $f_{T_0}(a)$ ถ้า $a_i$ มีค่าเป็น 0 และมีค่าเป็น $f_{T_1}(a)$ ถ้า $a_i$ มีค่าเป็น 1 รูปต่อไปนี้แสดงตัวอย่าง decision tree บนตัวแปร $x_1,x_2,x_3,x_4$ ซึ่งจะให้ค่าเป็น 1 หาก input เป็น $(0,1,1,0)$ แต่จะให้ค่าเป็น 0 หาก input เป็น $(1,0,1,1)$ สังเกตว่าตัวแปร $x_i$ แต่ละตัวอาจถูก label ที่ internal node ใน decision tree มากกว่าหนึ่ง node ก็ได้ อย่างไรก็ดี หากใน decision tree มี path จาก root ไปยัง leaf node ใด ที่มีตัวแปร $x_i$ บางตัวปรากฏมากกว่าหนึ่งครั้ง เราจะสามารถลดรูป decision tree ดังกล่าวให้ตัวแปรทั้งหมดปรากฏไม่เกินหนึ่งครั้งในแต่ละ path ได้
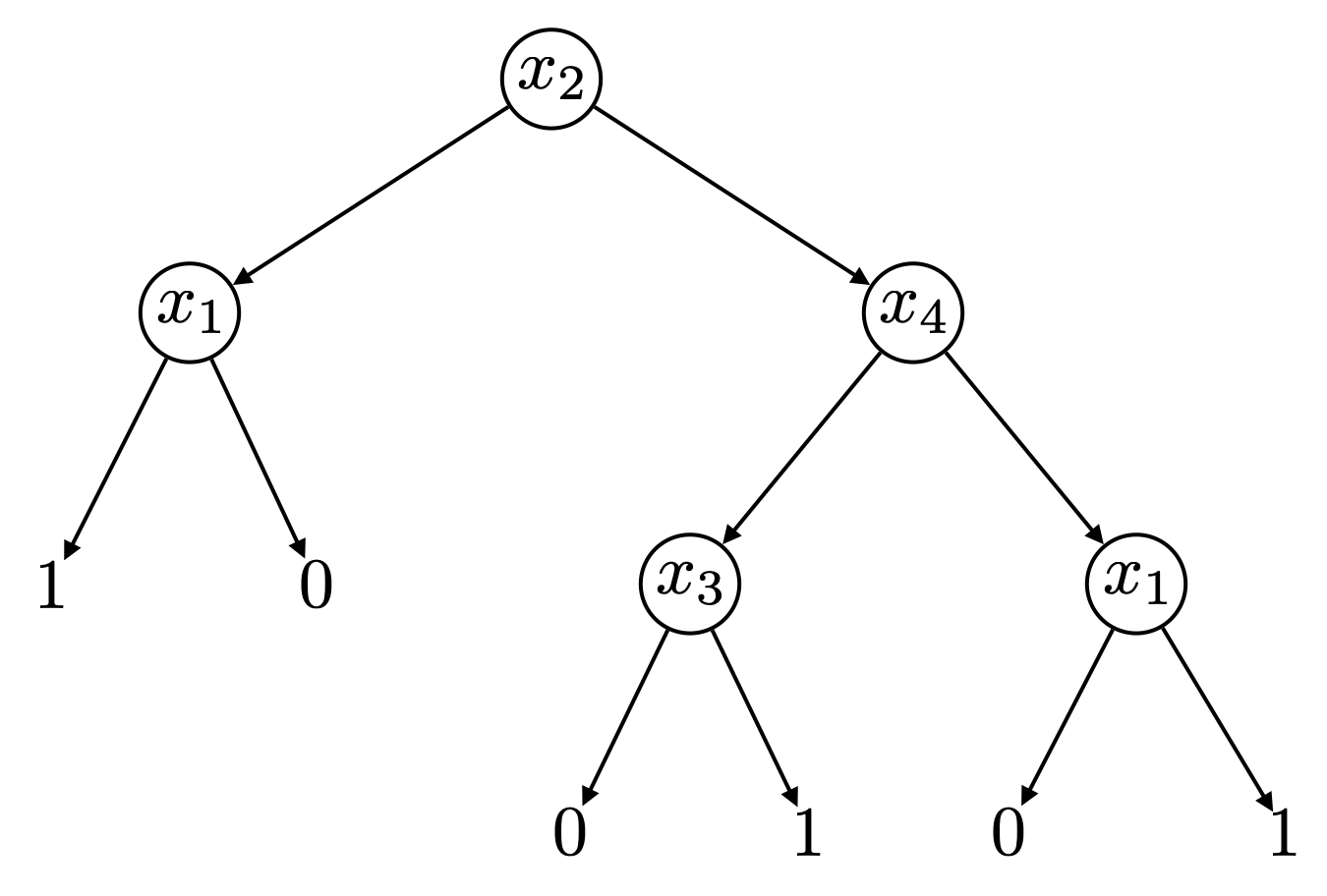
เราสามารถมองเห็นได้ไม่ยากนักว่า decision tree ต้นนี้ represent ฟังก์ชันที่แสดงได้ด้วย DNF ดังนี้
จากตัวอย่างนี้ สังเกตว่าหากเราให้ความสูงของ decision tree แทนจำนวน internal node ที่มากที่สุดใน path จาก root ไปยัง leaf node ใด ๆ เราจะได้ว่า ฟังก์ชันที่ represent ได้ด้วย decision tree ที่มีความสูงไม่เกิน $k$ จะสามารถ represent ด้วย $k$-DNF ได้เช่นกัน เราสามารถลดรูปจาก decision tree ความสูงไม่เกิน $k$ มาเป็น $k$-DNF ได้โดยการสร้าง conjunction หนึ่ง term สำหรับแต่ละ leaf ที่มี label เป็น 1 ซึ่ง conjunction ดังกล่าวประกอบด้วย $x_i$ หรือ $\bar{x}_i$ ที่อยู่ใน path จาก root มายัง leaf นั้น โดยการเลือก $x_i$ หรือ $\bar{x}_i$ พิจารณาจากทิศทางของ path ขณะที่ผ่าน node ที่ label ด้วย $x_i$ นั่นเอง ดังนั้นฟังก์ชันใด ๆ ที่ represent ด้วย decision tree ความสูงไม่เกิน $k$ ได้ก็จะสามารถ represent ด้วย $k$-DNF ได้เสมอ เราจึงสามารถสรุปตามมาได้ว่า ปัญหาการเรียนรู้ decision tree ที่มีความสูงไม่เกิน $k$ นั้นสามารถลดรูปให้เป็นปัญหาการเรียนรู้ $k$-DNF ได้ ซึ่งเรารู้ว่ากลุ่มของฟังก์ชันดังกล่าวสามารถเรียนรู้ได้โดยใช้ $k$-decision list เป็น representation
อย่างไรก็ดี การลดรูปจาก decision tree ความสูง $k$ ไปเป็น $k$-DNF ดังกล่าวอาจยังมีประสิทธิภาพไม่ดีนัก พิจารณาตัวอย่าง decision tree ความสูงเท่ากับ 3 ดังรูปต่อไปนี้
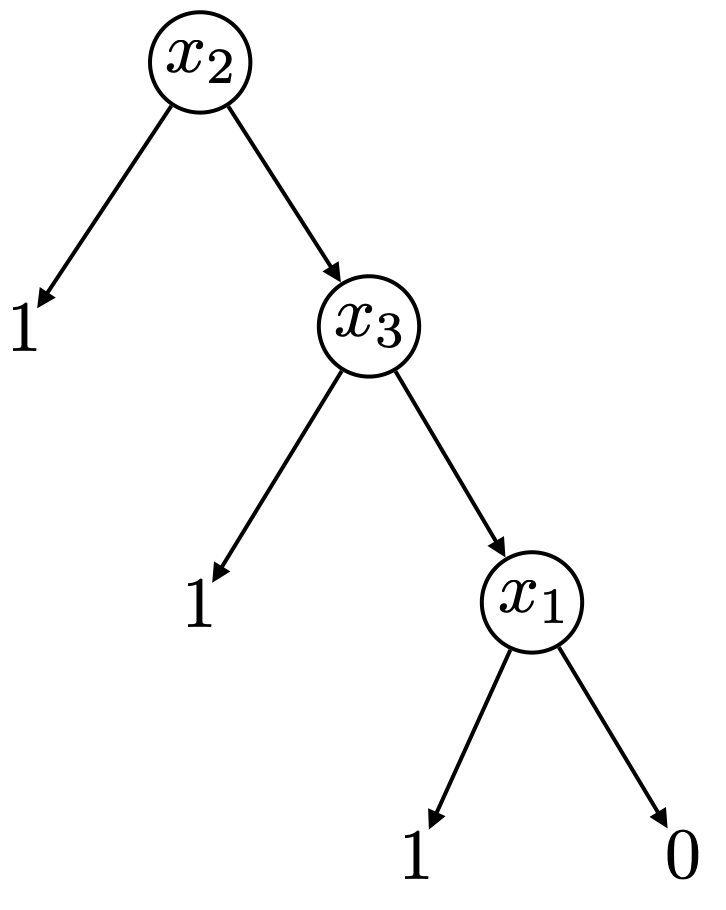
จะเห็นว่าด้วยวิธีการดังกล่าว เราจะสามารถลดรูปให้กลายเป็น 3-DNF
ซึ่ง represent ได้ด้วย 3-decision list ในขณะที่เราเห็นได้ชัดเจนว่า decision tree ต้นนี้มีลักษณะการตัดสินใจแบบเดียวกับ 1-decision list
จะเห็นว่าการแปลง decision tree เป็น 1-decision list นี้มีความเรียบง่ายกว่าและใช้พื้นที่ของ representation น้อยกว่าแบบก่อน ซึ่งนำไปสู่ประสิทธิภาพในการเรียนรู้ decision tree ที่ดีกว่า เนื่องจากถ้าเราสามารถลดรูปปัญหาการเรียนรู้ให้ concept class มีขนาดเล็กลงได้ ก็จะทำให้ประสิทธิภาพในการเรียนรู้ยิ่งดีขึ้น
Rank-$r$ decision tree represent ได้ด้วย $r$-decision list
ในหัวข้อนี้เราจะแสดงให้เห็นวิธีการแปลง decision tree ให้เป็น decision list ที่ represent ฟังก์ชันเดียวกัน โดย decision list ที่ได้จะมีขนาดของ representation ที่รัดกุมมากกว่าการแปลงเป็น DNF ก่อนหน้านี้ การแปลง representation ดังกล่าวจะทำให้เราสามารถเรียนรู้ decision tree ได้โดยใช้อัลกอริทึมในการเรียนรู้ decision list ได้ ซึ่งอัลกอริทึมดังกล่าวมีความเรียบง่ายเป็นอย่างมาก
สำหรับ decision tree $T$ เรานิยาม rank ของ $T$ ให้ $rank(T)$ มีค่าเป็น 0 ถ้า $T$ เป็นต้นไม้ที่มี node เดียว ไม่เช่นนั้นให้ $T_0$ และ $T_1$ เป็นต้นไม้ย่อยด้านซ้ายและขวาของ root ของ $T$ เรากำหนดให้
สังเกตว่า rank ของ decision tree $T$ จะบ่งบอกถึงความสมดุลของ $T$ โดยหาก $rank(T)$ มีค่าสูง แสดงว่า $T$ มีความสมดุลมาก และหาก $rank(T)$ มีค่าน้อย แสดงว่า $T$ มีความสมดุลต่ำ โดย $T$ ที่มี rank เป็น 1 นั้นมีลักษณะเป็น 1-decision list อย่างชัดเจน
เราจะแสดงให้เห็นว่าฟังก์ชันใดที่สามารถ represent ได้ด้วย decision tree ที่มี rank เท่ากับ $r$ จะสามารถ represent ด้วย $r$-decision list ได้เช่นกัน
ในขั้นแรก เราจะแสดงให้เห็นว่า decision tree $T$ ที่มี rank เท่ากับ $r$ นั้นจะต้องมี leaf บาง node ที่ห่างจาก root ไม่เกิน $r$ ในกรณีที่ $r=0$ สังเกตว่า $T$ จะเป็นต้นไม้ที่มีเพียง node เดียวซึ่งเป็นทั้ง root และ leaf เราก็จะได้ leaf node ที่มีระยะห่างจาก root เท่ากับ 0 ตามต้องการ สำหรับกรณีที่ $r>0$ เนื่องจาก $T$ มี rank เท่ากับ $r$ จากนิยามของ $rank(T)$ แสดงว่าจะต้องมีต้นไม้ย่อยด้านซ้ายหรือขวา ของ root ของ $T$ ที่มี rank ไม่เกิน $r-1$ สมมติให้ต้นไม้ย่อยดังกล่าวเป็น $T’$ จาก induction hypothesis เราจะได้ว่าจะต้องมี leaf ของ $T’$ อย่างน้อยหนึ่ง node ที่ห่างจาก root ของ $T’$ ไม่เกิน $r-1$ เมื่อเราเพิ่มเส้นเชื่อมจาก root ของ $T$ ไปยัง root ของ $T’$ เข้าไปใน path ดังกล่าว เราก็จะได้ path จาก root ของ $T$ ไปยัง leaf ของ T ที่มีความยาวไม่เกิน $r$ ตามต้องการ ดังนั้นเราจึงสรุปได้ว่า rank-$r$ decision tree ใด ๆ จะต้องมี leaf บาง node ที่ห่างจาก root ไม่เกิน $r$ แน่นอน
คราวนี้เราจะแสดงให้เห็นว่าสำหรับ rank-$r$ decision tree $T$ ใด ๆ จะต้องมี $r$-decision list $L$ ที่ represent ฟังก์ชันเดียวกัน โดยถ้าให้ $m$ เป็นจำนวน leaf ของ $T$ เราจะแสดงการสร้าง $r$-decision list ดังกล่าวที่มีจำนวน conjunction ที่ใช้เป็นเงื่อนไขไม่เกิน $m$
เราจะแสดงด้วย induction บนค่าของ $m$ และ $r$ โดยในขั้นตอนแรก เมื่อ $m=2$ จะเห็นว่า $T$ จะต้องมี rank เท่ากับ 1 และเราสามารถสร้าง 1-decision list $L$ ที่สอดคล้องกับ $T$ ได้อย่างง่าย ถัดมา สำหรับ $T$ ที่มี rank เท่ากับ $r$ ใด ๆ และมีจำนวน leaf เป็น $m$ เรารู้ว่าจะต้องมี leaf node $l$ ที่อยู่ห่างจาก root ไม่เกิน $r$ สมมติให้ระยะห่างดังกล่าวเท่ากับ $k\leq r$ และให้ $u_1,\dots,u_k$ แทน internal node ทั้งหมดใน path จาก root ไปยัง $l$ โดยมีตัวแปร $x_{i_1},\dots,x_{i_k}$ ถูก label อยู่ตามลำดับ เราจะให้ $y_1,\dots,y_k$ เป็นลำดับของ literal โดย $y_j$ เป็น literal ของ $x_{i_j}$ ที่จะต้องมีค่าเป็นจริงในการกำหนดค่าใด ๆ ที่จะผ่าน $u_j$ ไปยัง $l$ ตัวอย่างเช่น ถ้า $l$ เป็นลูกด้านขวาของ $u_k$ เราจะให้ $y_k=x_{i_k}$ และถ้า $l$ เป็นลูกด้านซ้ายของ $u_k$ เราจะให้ $y_k=\bar{x}_{i_k}$ จากนั้น ถ้า $l$ ถูก label ด้วย เราจะได้ว่าการกำหนดค่าใดที่ทำให้ conjunction เป็นจริง จะมีคำตอบที่ถูกต้องเป็น $b$ ดังนั้นเราสามารถเพิ่ม $(y_1\dots y_k, b)$ เป็นคู่ลำดับแรกใน $L$
คราวนี้กำหนดให้ $u_{k+1}$ เป็น node ลูกอีก node หนึ่งของ $u_k$ พิจารณาการกำหนดค่า $a$ ที่ทำให้การหาคำตอบของ input $a$ ใน $L$ ไม่ได้สิ้นสุดที่เงื่อนไขแรก ถ้า $y_1y_2\dots y_{k-1}$ เป็นจริงใน $a$ แสดงว่า $y_k$ จะต้องไม่เป็นจริงแน่นอน ดังนั้นจะเห็นว่าเงื่อนไขใน $L$ หลังจากนี้ไม่จำเป็นต้องสนใจ node $u_k$ อีกต่อไป นั่นคือ เราสามารถหาองค์ประกอบมาต่อท้ายใน $L$ เพิ่มเติม โดยพิจารณาจาก decision tree $T’$ ที่ลบ node $l$ และ $u_k$ ออกไป และเชื่อม node $u_{k-1}$ ไปยัง $u_{k+1}$ โดยตรง ซึ่งจะเห็นว่า $T’$ นั้นจะมีจำนวน leaf เหลือเป็น $m-1$ นอกจากนี้ $T’$ จะมี rank ไม่เกิน $r$ เนื่องจาก rank ของต้นไม้ย่อยที่มี $u_{k+1}$ เป็น root จะไม่มีทางมากกว่า rank ของต้นไม้ย่อยที่มี $u_k$ เป็น root ดังนั้นหลังจากที่เราเชื่อมให้ $u_{k+1}$ มาเป็นลูกของ $u_{k-1}$ จะไม่ทำให้ rank ของต้นไม้ย่อยที่มี $u_{k-1}$ เป็น root เพิ่มขึ้นจากเดิม และได้ว่า rank ของ $T’$ ก็ต้องไม่เพิ่มขึ้นจาก $r$ ด้วยเช่นกัน ถึงตรงนี้เราสามารถอ้างจาก induction hypothesis ได้ว่า $T’$ ที่มี rank เป็น $r’\leq r$ ก็จะมี $r’$-decision list $L’$ ที่ represent ฟังก์ชันเดียวกันโดยใช้จำนวน conjunction ที่เป็นเงื่อนไขไม่เกิน $m-1$ เมื่อเรานำ $L’$ มาต่อท้ายคู่ลำดับแรกของเรา ก็จะได้ $r$-decision list $L$ ความยาวไม่เกิน $m$ ที่ represent ฟังก์ชันเดียวกับ $T$ ตามต้องการ
เราจึงสามารถสรุปได้ว่าเซตของฟังก์ชันที่ represent ได้ด้วย rank-$r$ decision tree จะเป็นสับเซตของ $r$-DL ดังนั้น หากเราต้องการเรียนรู้ฟังก์ชันบางอย่างที่เรารู้ว่าอยู่ในรูปของ decision tree โดยที่เราไม่สนใจ representation เราก็สามารถใช้อัลกอริทึมในการเรียนรู้ decision list แก้ปัญหานี้ได้ อย่างไรก็ดี ในความเป็นจริงแล้วปัญหาการเรียนรู้ decision tree นี้ก็สามารถเรียนรู้ได้อย่างมีประสิทธิภาพ นั่นคือ หากเรายังคงต้องการ representation ในรูปของ decision tree เราก็สามารถออกแบบอัลกอริทึมที่อาจซับซ้อนมากขึ้น เพื่อหา decision tree ที่สอดคล้องกับตัวอย่างข้อมูลทั้งหมดที่ได้รับมาได้เช่นกัน