ปัญหาการเรียนรู้ Decision List

เป้าหมายหนึ่งในการศึกษาด้านการเรียนรู้นั้น คือการหา concept class ที่สามารถเรียนรู้ได้อย่างมีประสิทธิภาพที่มีความเป็นทั่วไปให้ได้มากที่สุด กล่าวคือ เราอยากจะหา concept class ที่เรียนรู้ได้ที่ครอบคลุม concept จำนวนมากที่สุดเท่าที่เป็นไปได้ ในหัวข้อนี้เราจะมาดูเทคนิคใหม่ในการ represent concept ในกลุ่ม boolean formula ที่เรียกว่า decision list ซึ่งเราจะได้เห็นว่าสามารถ represent concept ได้กว้างกว่า concept class ที่เคยศึกษามา และที่สำคัญคือสามารถเรียนรู้ได้อย่างมีประสิทธิภาพอีกด้วย

นิยาม decision list

decision list บนตัวแปร $x_1,\dots,x_n$ คือรายการ (list) $L$ ของคู่ลำดับ

และบิต $v\in\{0,1\}$ เมื่อ $f_i$ ใด ๆ เป็น boolean conjunction บนตัวแปร $x_1,\dots,x_n$ และ $v_i\in\{0,1\}$

สำหรับการกำหนดค่า $a\in \{0,1\}^n$ ใด ๆ เราจะให้ค่าของ $L(a)$ มีค่าเท่ากับ $v_j$ เมื่อ $j$ เป็นลำดับที่น้อยที่สุดที่ $f_j(a)=1$ ถ้าไม่มี conjunction $f_i$ ใดที่การกำหนดค่าใน $a$ ทำให้เป็น 1 ได้เลย เราจะให้ $L(a)=v$

เราสามารถมอง decision list ในรูปของลำดับการตัดสินใจแบบ if - then - else if - then - ... else - ได้ดังนี้

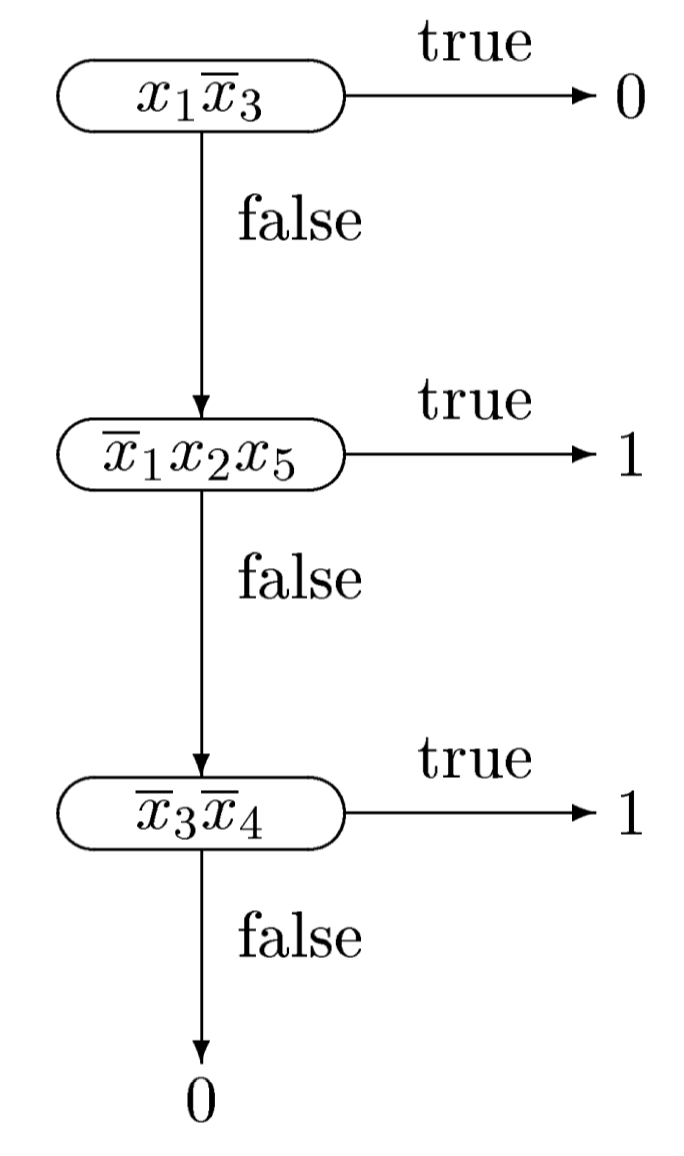
ตัวอย่างเช่น decision list ที่มีรายการของคู่ลำดับดังนี้

และมี $v=0$ เมื่อรับการกำหนดค่า $a_1=(0,1,0,0,1)$ จะให้ผลลัพธ์เป็น 1 โดยอ้างอิงจาก conjunction $\bar{x}_1x_2x_5$ ในขณะที่ $a_2=(0,0,1,1,1)$ จะให้ผลลัพธ์เป็น 0 ตามค่า $v$ เนื่องจาก $a_2$ ไม่สามารถทำให้ conjunction ใดในรายการนี้เป็นจริงได้เลย เราอาจมอง decision list ในลักษณะแผนภาพได้ตามภาพต่อไปนี้

เรากำหนดให้ $k$-decision list คือ decision list ที่ conjunction ทุกตัวในรายการมีจำนวน literal ไม่เกิน $k$ และให้ $k$-DL เป็นเซตของฟังก์ชันทั้งหมดที่แทนได้ด้วย $k$-decision list สังเกตว่า สำหรับฟังก์ชัน $c$ ใด ๆ ใน $k$-DL เราจะได้ว่า $\neg c$ หรือ complement ของ $c$ ก็อยู่ใน $k$-DL ด้วยเช่นกัน โดยเราสามารถสร้าง $k$-decision list ที่ represent $\neg c$ ได้โดยนำ $k$-decision list ของ $c$ มาสลับค่าของ $v$ และ $v_i$ ทั้งหมด

ความเป็นทั่วไปของ decision list

ในหัวข้อนี้ เราจะแสดงให้เห็นว่า boolean function ใด ๆ ในรูปแบบต่าง ๆ เช่น $k$-CNF, $k$-DNF, $k$-clause CNF และ $k$-term DNF นั้นสามารถ represent ด้วย $k$-decision list ได้ทั้งหมด หมายความว่า decision list นั้นสามารถนำเสนอฟังก์ชันได้กว้างกว่ารูปแบบที่เราเคยรู้จักมานั่นเอง

ก่อนอื่นเราจะมาทบทวน boolean formula ในรูปแบบต่าง ๆ กันก่อน เราจะเรียก boolean formula ว่าเป็น conjunctive normal form (CNF) ถ้าเป็น conjunction (and) ของ clause โดยที่แต่ละ clause เป็น disjunction (or) ของ literal ถ้าทุก clause มีจำนวน literal ไม่เกิน $k$ เราจะเรียก CNF นั้นว่าเป็น $k$-CNF ในขณะที่ถ้า CNF ที่เราสนใจมีจำนวน clause เท่ากับ $k$ เราก็จะเรียกว่าเป็น $k$-clause CNF

ในทำนองเดียวกัน disjunctive normal form (DNF) คือเซตของ boolean formula ที่อยู่ในรูป disjunction (or) ระหว่าง term ต่าง ๆ โดยที่แต่ละ term จะเป็น conjunction (and) ของ literal เราจะใช้ $k$-DNF แทนเซตของ DNF ที่ทุก term มีจำนวน literal ไม่เกิน $k$ และใช้ $k$-term DNF แทนเซตของ DNF ที่มีจำนวน term เท่ากับ $k$

ในทางตรรกศาสตร์เราสามารถพิสูจนได้ว่าสำหรับฟังก์ชันใด ๆ จะเขียนในรูป $k$-CNF ได้ก็ต่อเมื่อ negation ของฟังก์ชันนั้นสามารถเขียนในรูป $k$-DNF ได้ ตัวอย่างเช่น negation ของ 2-CNF ต่อไปนี้

จะเป็น 2-DNF ตามนี้

ในทำนองเดียวกัน เราสามารถแสดงได้ว่าฟังก์ชันใดจะเขียนในรูป $k$-term DNF ได้ก็ต่อเมื่อ negation ของมันสามารถเขียนในรูป $k$-clause CNF ได้

นอกจากนี้ เราสามารถแสดงได้ว่าเซต $k$-term DNF นั้นเป็นสับเซตของ $k$-CNF เนื่องจากเราสามารถจัดรูปฟังก์ชันที่เป็น $k$-term DNF ให้เป็น $k$-CNF ได้เสมอ ตัวอย่างเช่น

เป็น 3-term DNF ที่สามารถจัดรูปใหม่เป็น 3-CNF ได้ดังนี้

และสำหรับ $k$-clause CNF ใด ๆ เราก็สามารถจัดรูปใหม่ให้เป็น $k$-DNF ได้เสมอเช่นกัน

ในการแสดงความเป็นทั่วไปของ decision list เราจะเริ่มจากการแสดงให้เห็นว่าฟังก์ชัน $f$ ใด ๆ ในเซต $k$-DNF นั้นจะอยู่ในเซต $k$-DL ด้วยเสมอ โดยสมมติให้ $f$ จัดในรูป $k$-DNF ได้เป็น

เมื่อ $T_i$ เป็น conjunction ที่มีจำนวน literal ไม่เกิน $k$ การสร้าง $k$-decision list ที่ represent ฟังก์ชันเดียวกับ $f$ นั้นทำได้โดยนำแต่ละ term $T_i$ มาสร้างเป็นคู่ลำดับใน decision list ที่มีผล $v_i=1$ และกำหนดให้ผล default $v=0$ สังเกตว่าถ้าการกำหนดค่า $a$ ทำให้ $f$ เป็นจริง แสดงว่าจะต้องมี term $T_i$ ที่ $a$ ทำให้เป็นจริงได้ ดังนั้น ใน decision list ของเรา เมื่อ $a$ ทำให้ $T_i$ เป็นจริง ก็จะได้ผลเป็น $v_i=1$ ในขณะที่หาก $a$ ไม่สามารถทำให้ $f$ เป็นจริงได้ แสดงว่าจะต้องไม่มี term $T_i$ ใด ๆ ที่ $a$ ทำให้เป็นจริงได้เลย เมื่อนำ $a$ มาเป็น input ให้กับ decision list ก็จะไม่สอดคล้องกับเงื่อนไขใดเลย นั่นคือ เราจะได้ผลเป็นค่า default $v=0$ น่ันเอง

ถัดมา เราสามารถแสดงให้เห็นว่าฟังก์ชัน $f$ ใด ๆ ที่อยู่ในรูป $k$-CNF นั้นก็สามารถ represent ด้วย $k$-decision list ได้เช่นกัน เนื่องจากฟังก์ชันใด ๆ ในรูป $k$-CNF นั้นจะมี complement ที่อยู่ในรูป $k$-DNF เนื่องจาก $k$-DL นั้นสามารถ represent ฟังก์ชันใน $k$-DNF ได้ และ $k$-DL มีสมบัติปิดภายใต้ complement

คราวนี้ เนื่องจาก $k$-clause CNF ใด ๆ สามารถ represent ในรูป $k$-DNF ได้ และ $k$-term DNF ใด ๆ สามารถ represent ในรูป $k$-CNF ได้ เราจึงสรุปได้ว่า $k$-clause CNF และ $k$-term DNF ก็เป็นสับเซตของ $k$-DL ด้วยเช่นกัน

ในความเป็นจริงแล้ว เราสามารถแสดงได้ว่ามีฟังก์ชันที่ represent ได้ด้วย $k$-decision list ที่ไม่สามารถ represent ด้วย $k$-CNF หรือ $k$-DNF ได้อีกด้วย นั่นแสดงให้เห็นชัดเจนยิ่งขึ้นว่าการนำเสนอฟังก์ชันทาง boolean ด้วย decision list นั้นมีพลังมากกว่ารูปแบบอื่น ๆ ที่เราได้รู้จักกันมา

อัลกอริทึมการเรียนรู้ $k$-DL

คราวนี้เราจะแสดงให้เห็นว่าปัญหาการเรียนรู้ $k$-DL นี้สามารถเรียนรู้ได้อย่างมีประสิทธิภาพตามแนวทางของ consistent hypothesis โดยเราจะเริ่มจากการแสดงวิธีหา $k$-decision list ที่สอดคล้องกับตัวอย่างข้อมูลทั้งหมด

เพื่อความง่าย เราจะแสดงอัลกอริทึมการเรียนรู้สำหรับปัญหา 1-DL ก่อน โดยที่สำหรับค่า $k$ ใด ๆ นั้นเราสามารถลดรูปปัญหามาเป็น 1-DL ได้เช่นเดียวกับการลดรูปปัญหาการเรียนรู้ $k$-CNF ให้เป็นปัญหาการเรียนรู้ conjunction ที่ได้กล่าวถึงไปแล้วในหัวข้อ Representation และประสิทธิภาพในการเรียนรู้

ให้ $S=\{(a_1,y_1),\dots,(a_m,y_m)\}$ เป็นเซตของตัวอย่างข้อมูลที่สอดคล้องกับ 1-decision list $c$ บางตัว อัลกอริทึมของเราจะเริ่มจาก decision list ที่ไม่มีเงื่อนไขใด ๆ และทำการวนรอบเพิ่มเงื่อนไขที่เป็น literal $z$ พร้อมกับผล $v$ โดยในแต่ละรอบ สำหรับ literal $z$ ใด ๆ เราจะให้ $S_z\subseteq S$ เป็นเซตของตัวอย่างข้อมูลใน $S$ ที่สอดคล้องกับ $z$ เราจะทำการหา literal $z$ ที่สมาชิกทุกตัวใน $S_z$ เป็น positive example ทั้งหมด หรือไม่ก็เป็น negative example ทั้งหมด เมื่อได้ literal $z$ ดังกล่าวแล้ว ก็จะทำการเพิ่มคู่ลำดับ $(z,v_z)$ เข้าไปท้าย decision list ปัจจุบัน โดยที่ $v_z=1$ ถ้าสมาชิกใน $S_z$ เป็น positive example ทั้งหมด และ $v_z=0$ ถ้าเป็น negative example จากนั้นลบตัวอย่างข้อมูลใน $S_z$ ออกจาก $S$ แล้ววนรอบเลือก literal ดังกล่าวใหม่ จนกระทั่งสมาชิกที่เหลือใน $S$ เป็น positive example ทั้งหมด หรือเป็น negative example ทั้งหมด เราก็จะเพิ่มค่า default $v$ ที่สอดคล้องกันไปยัง decision list โดยไม่ต้องมีเงื่อนไขกำหนด

เราสามารถรับประกันได้ว่าในแต่ละรอบของอัลกอริทึม เราจะสามารถหา literal $z$ ตามต้องการได้เสมอ เนื่องจากตัวอย่างข้อมูลทั้งหมดใน $S$ ของเราจะต้องสอดคล้องกับ decision list เป้าหมาย $c$ ดังนั้นอย่างน้อยที่สุด เราจะต้องมี literal $z_{c,1}$ ที่เป็นเงื่อนไขแรกใน $c$ ที่ตัวอย่างข้อมูลทั้งหมดที่สอดคล้องกับ $z_{c,1}$ อยู่ในกลุ่มเดียวกัน (เป็น positive example เหมือนกันทั้งหมด หรือเป็น negative example เหมือนกันทั้งหมด) หากอัลกอริทึมของเราเลือกได้ literal ตัวอื่น เราก็รับประกันได้ว่าจะมี $z_{c,1}$ ให้เลือกในรอบต่อไป แต่ถ้าอัลกอริทึมของเราเลือกได้ $z_{c,1}$ มาก่อนแล้ว ให้ $z_{c,i}$ เป็น literal ที่ใช้เป็นเงื่อนไขใน $c$ ที่มีลำดับน้อยที่สุดที่ยังไม่ถูกเลือกในอัลกอริทึมของเรา จะเห็นว่าตัวอย่างข้อมูลที่เหลือใน $S$ ที่สอดคล้องกับ $z_{c,i}$ ก็จะต้องอยู่ในกลุ่มเดียวกันแน่นอน ดังนั้นเราจึงมั่นใจได้ว่าอัลกอริทึมของเราจะสามารถหา literal ตามต้องการได้จนกระทั่งสิ้นสุดการทำงาน

เนื่องจาก literal บนตัวแปร $n$ ตัวสามารถระบุได้โดยใช้พื้นที่ $\log_2 2n$ บิต และ 1-decision list ของเราจะมีจำนวนเงื่อนไขไม่เกิน $2n$ ตัว ดังนั้นเราสามารถระบุ 1-decision list บนตัวแปร $n$ ตัวได้โดยใช้พื้นที่เป็น $O(n\log n)$ จากหลักในการเรียนรู้ด้วย consistent hypothesis เราจะสามารถเรียนรู้ปัญหา 1-DL ได้ด้วย sample complexity

หรือได้ว่า hypothesis $h$ ที่ได้จะมี generalization error เป็น

นั่นเอง

สังเกตว่าในการทำงานแต่ละรอบของอัลกอริทึมการเรียนรู้นี้ หากมี literal ตามต้องการมากกว่าหนึ่งตัว อัลกอริทึมของเราเปิดทางเลือกให้เลือกตัวใดมาใช้ก็ได้ ซึ่งจะเห็นว่าหากเรามีวิธีการเลือกที่ดีก็อาจทำให้ได้ decision list ที่มีจำนวนเงื่อนไขน้อย แนวทางหนึ่งที่น่าสนใจคือการใช้แนวคิดแบบ greedy นั่นคือ ในแต่ละรอบเราจะเลือก literal $z$ ที่ $S_z$ มีขนาดใหญ่ที่สุดมาเป็นเงื่อนไข อย่างไรก็ดี การหา decision list ที่สั้นที่สุดที่สอดคล้องกับตัวอย่างข้อมูลทั้งหมดใน $S$ นั้น จัดเป็นปัญหาที่อยู่ในกลุ่มปัญหา NP-complete

Prev: การเรียนรู้ Boolean Conjunction ด้วย Inconsistent Hypothesis

Next: Decision Tree