Growth Function

หลังจากที่เราได้รู้จัก dichotomy กันมาแล้ว สังเกตว่าเมื่อเรากำหนดเซตของตัวอย่างข้อมูลไว้ hypothesis space แต่ละตัวอาจมีจำนวน dichotomy แตกต่างกันได้ โดย hypothesis space ที่มีความซับซ้อนมากก็จะสามารถสร้างจำนวน dichotomy ได้มากกว่า hypothesis space ที่มีความซับซ้อนน้อย จากตรงนี้ทำให้เราเห็นว่า จำนวน dichotomy ที่สร้างได้จาก hypothesis space นั้นสามารถเป็นตัวแทนในการบอกความซับซ้อนของ hypothesis space ที่เราสนใจได้ จึงเป็นที่มาของ growth function ซึ่งมีนิยามดังนี้

นิยาม growth function ของ hypothesis space $H$ บนข้อมูล $m$ ตัว เขียนแทนด้วย $\Pi_H(m)$ มีค่าเท่ากับ

หรือกล่าวได้ว่า $\Pi_H(m)$ คือจำนวน dichotomy ที่มากที่สุดบนตัวอย่างข้อมูล $m$ จุดใด ๆ ที่สามารถสร้างได้จาก $H$ โดยในการคำนวณ $\Pi_H(m)$ นั้น เราต้องพิจารณาตัวอย่างข้อมูล $m$ จุดทุกรูปแบบ และตอบจำนวน dichotomy ของรูปแบบที่จำแนกได้หลากหลายที่สุด สังเกตว่า $\Pi_H(m)$ นี้จะเป็นเหมือนขอบเขตบนของขนาดของ $H$ เมื่อ input space ของเราเป็น subspace ของ $X$ ที่มีขนาดเท่ากับ $m$ ซึ่งจะเห็นว่าสำหรับ $H$ ใด ๆ

เพื่อทำความเข้าใจ growth function ให้มากขึ้น เราจะมาดูตัวอย่าง hypothesis space ง่าย ๆ ดูเล็กน้อย

Positive rays

กำหนดให้ $X=\mathbb{R}$ และให้ $H_1$ เป็นเซตของฟังก์ชัน $h:\mathbb{R}\to\{0,1\}$ ที่อยู่ในรูป

หรือก็คือ

เมื่อ $a\in\mathbb{R}$ นั่นคือ hypothesis ใน $H_1$ จะทำการจำแนกจำนวนจริงออกเป็นสองคลาส โดยให้จำนวนจริงใด ๆ ที่น้อยกว่าค่า $a$ ที่กำหนดไว้เป็นคลาส 0 และจำนวนจริงตั้งแต่ $a$ ขึ้นไปเป็นคลาส 1

ในการคำนวณ $\Pi_{H_1}(m)$ นั้น สังเกตว่าเมื่อเราได้รับตัวอย่างข้อมูล $m$ ตัว ถ้าตัวอย่างข้อมูลนั้นแตกต่างกันทั้งหมด จะได้ว่าตัวอย่างข้อมูลเหล่านั้นแบ่งพื้นที่บนเส้นจำนวนออกเป็น $m+1$ ส่วนดังรูปต่อไปนี้ และเมื่อเรานำ $a$ ไปวางไว้ในแต่ละส่วน ก็จะทำให้ได้ dichotomy ที่ต่างกันออกไป ในขณะที่สำหรับฟังก์ชัน $h$ ใด ๆ ที่ $a$ อยู่ในบริเวณเดียวกัน จะทำให้ได้ dichotomy เดียวกัน ดังนั้นเราจึงได้ว่าจำนวน dichotomy ทั้งหมดที่สร้างได้จาก $H_1$ เท่ากับ $m+1$

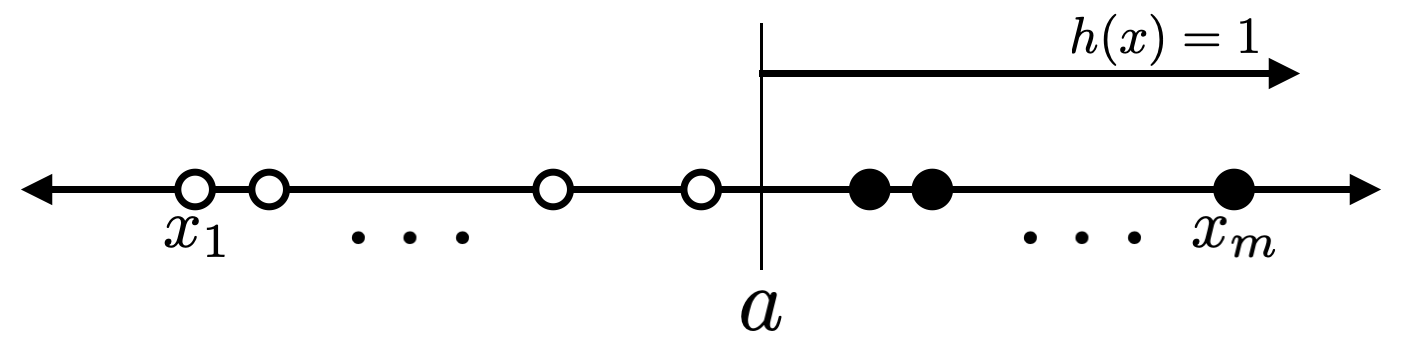
สังเกตว่าหากในตัวอย่างข้อมูลของเรามีข้อมูล $x_i$ และ $x_j$ บางคู่ที่ $i\neq j$ แต่ $x_i=x_j$ จะทำให้เราสร้าง dichotomy ได้จำนวนน้อยกว่า $m+1$ อย่างไรก็ดี เนื่องจากในนิยามของ growth function นั้น เรานับจำนวน dichotomy ที่มากที่สุดที่เป็นไปได้ ดังนั้นเราจึงได้ว่า

Positive Intervals

คราวนี้ให้ $X=\mathbb{R}$ เช่นเดิม และให้ $H_2$ เป็นเซตของ hypothesis ที่ตอบคลาส 1 สำหรับค่า $x$ ที่อยู่ในช่วง $[a,b]$ และตอบคลาส 0 สำหรับกรณีอื่น ๆ รูปต่อไปนี้แสดงตัวอย่าง hypothesis $h\in H_2$

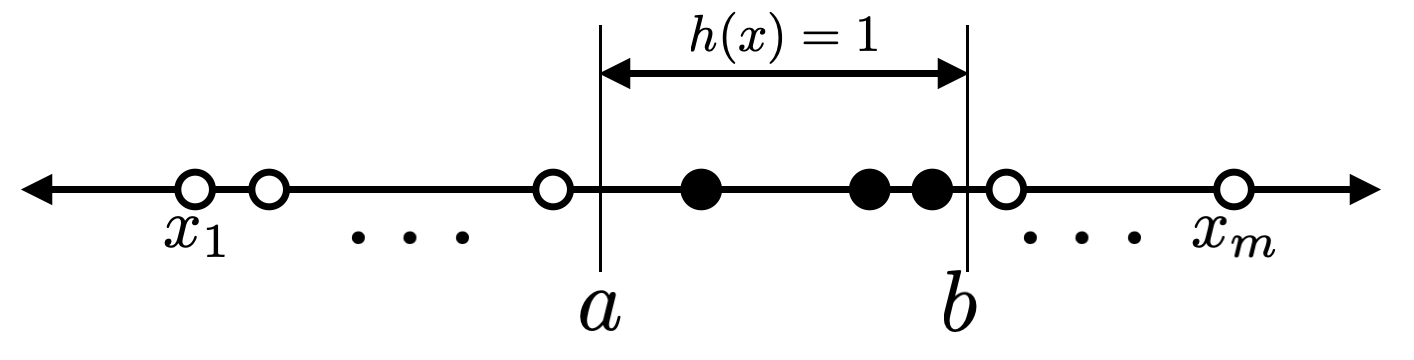
ในการคำนวณ $\Pi_{H_2}(m)$ สำหรับกรณีนี้ จะเห็นว่าตัวอย่างข้อมูล $m$ ตัวนั้นจะแบ่งพื้นที่ในเส้นจำนวนให้เราเป็น $m+1$ ส่วนเช่นเดิม สังเกตว่าจำนวน dichotomy ที่แตกต่างกันนั้นเกิดจากวิธีการเลือกส่วนของเส้นจำนวนให้กับจุด $a$ และ $b$ โดยในกรณีที่ $a$ และ $b$ ไม่ได้ตกอยู่ในส่วนเดียวกัน จะเป็นไปได้ทั้งสิ้น ${m+1 \choose 2}$ วิธี และในกรณีที่ $a$ และ $b$ ตกอยู่ในส่วนเดียวกัน สังเกตว่าไม่ว่า $a$ และ $b$ จะตกอยู่ในส่วนใดก็ตาม หากตกอยู่ในส่วนเดียวกันเราจะได้ dichotomy รูปแบบเดียวกัน นั่นคือ dichotomy ที่ตอบคลาส 0 สำหรับตัวอย่างข้อมูลทั้ง $m$ ตัว

ดังนั้นเราจึงได้ว่า

จะเห็นว่าอัตราการโตของ growth function $\Pi_{H_2}(m)$ สำหรับ $H_2$ นั้นเป็น $O(m^2)$ ซึ่งโตเร็วกว่า $\Pi_{H_1}(m)$ ของ $H_1$ ที่มีความซับซ้อนน้อยกว่า

Convex sets

คราวนี้เรามาลองดูตัวอย่างที่ซับซ้อนมากขึ้น พิจารณาเมื่อ $X=\mathbb{R}^2$ และ $H$ เป็นเซตของ hypothesis $h:\mathbb{R}^2\to\{0,1\}$ ที่ให้ผลเป็น 1 สำหรับจุดที่อยู่ในพื้นที่ convex set ที่กำหนด และให้ผลเป็น 0 สำหรับจุดที่อยู่นอก convex set ดังกล่าว โดยที่เรานิยามให้ convex set คือเซตที่ส่วนของเส้นตรงใด ๆ ที่เชื่อมระหว่างสองจุดภายในเซตจะต้องอยู่ภายในเซตด้วยเช่นกัน

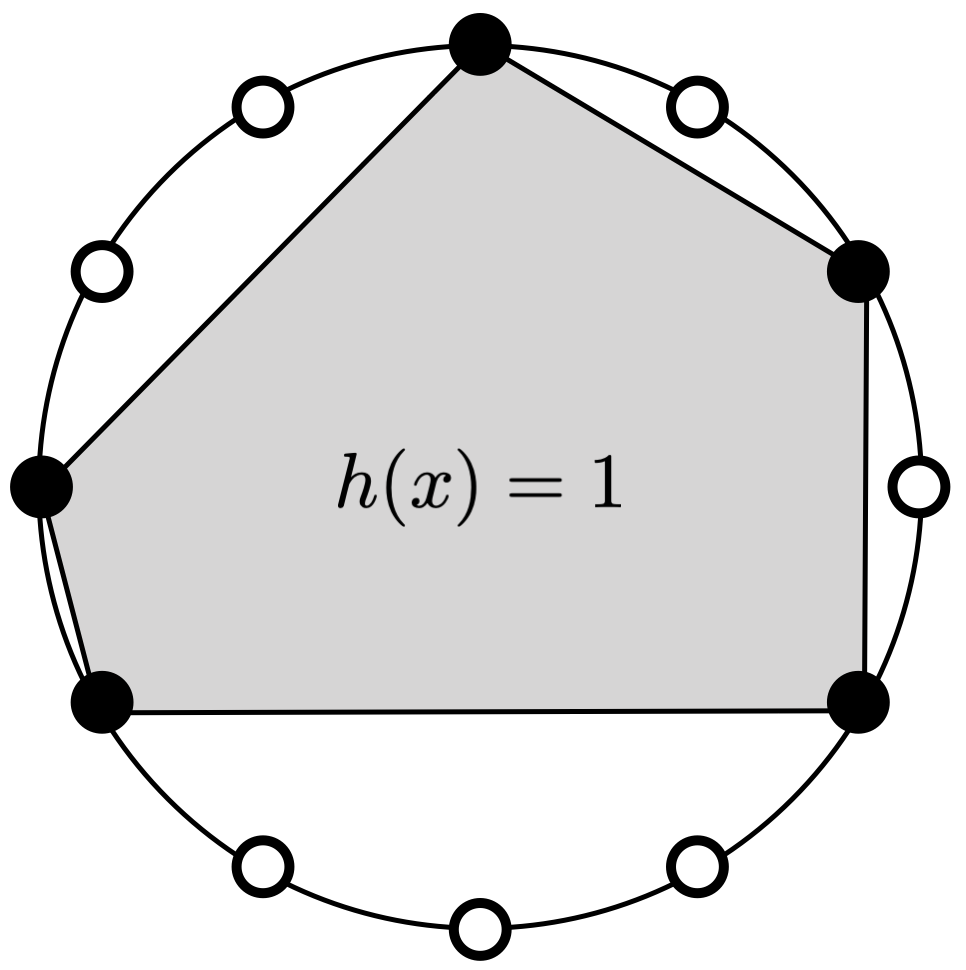
ในการคำนวณ $\Pi_H(m)$ ในกรณีนี้เราต้องเลือกตำแหน่งของตัวอย่างข้อมูลทั้ง $m$ จุดอย่างระมัดระวัง เพื่อที่จะให้ได้จำนวน dichotomy มากที่สุด วิธีหนึ่งที่ทำได้ไม่ยากนัก คือการกำหนดให้จุดทั้ง $m$ จุดเรียงอยู่บนเส้นรอบวงของวงกลมวงหนึ่ง สังเกตว่าสำหรับ dichotomy ใด ๆ บนจุดทั้ง $m$ จุดนี้ เราจะสามารถสร้าง convex set ที่ครอบคลุมเฉพาะ positive example ใน dichotomy นั้นได้เสมอโดยลากส่วนของเส้นตรงเชื่อม positive example ที่อยู่เรียงต่อกันบนแนวเส้นรอบวงจนกระทั่งได้เป็นรูปปิดที่มี positive example แต่ละตัวเป็นจุดมุม (ดูรูปด้านล่างประกอบ) ด้วยวิธีนี้จะเห็นว่าเราสามารถสร้าง convex set ที่สอดคล้องกับ dichotomy ได้ทุกรูปแบบ นั่นแสดงว่าจำนวน dichotomy ที่สามารถสร้างได้จาก $H$ ก็คือ

นั่นเอง

ถึงแม้ว่าเราสามารถคำนวณ growth function ได้สำหรับ hypothesis space ในตัวอย่างทั้งสามนี้ ในความเป็นจริงแล้ว hypothesis space ที่ใช้จริงในทางปฏิบัติมักจะคำนวณ growth function ได้ยาก อย่างไรก็ดี ในการวิเคราะห์ความสามารถในการเรียนรู้นั้น เราไม่จำเป็นต้องรู้ growth function อย่างชัดเจน หากเรารู้ขอบเขตของ growth function ก็สามารถนำขอบเขตนั้นไปวิเคราะห์แทนได้เช่นกัน เราจะได้เห็นกันต่อไปว่าเราสามารถแสดงขอบเขตของ growth function ให้อยู่ในรูปของ VC-dimension ได้

Prev: Dichotomy

Next: VC-Dimension