Sample complexity

จากหัวข้อที่แล้ว เราได้ทำการวิเคราะห์ generalization bound ของ risk ของ hypothesis ที่ได้จากการเรียนรู้โดยขึ้นอยู่กับจำนวนตัวอย่างข้อมูลที่ใช้เทรนและ VC dimension กันมาแล้ว ในหัวข้อนี้เราจะมาวิเคราะห์ในมุมของ sample complexity กันดูบ้างว่าหากเราต้องการได้ hypothesis ที่มี risk แตกต่างจาก hypothesis ที่ดีที่สุดไม่เกิน $\epsilon$ ด้วยความน่าจะเป็นสูง เราจะต้องการตัวอย่างข้อมูลใน training set มากแค่ไหน

ในกรณีที่เราสามารถหา hypothesis ที่ consistent กับตัวอย่างข้อมูล $S=\{(x_1,y_1),\dots,(x_m,y_m)\}$ ได้เสมอ จากการวิเคราะห์ generalization bound ในหัวข้อก่อน เราจะได้ว่า

$\Pr[\exists h\in H: R(h)>\epsilon \text{ และ } h \text{ consistent กับ } S]\leq 2\left(\frac{2em}{d}\right)^d2^{-\epsilon m/2}$

ดังนั้นหากเราต้องการให้เหตุการณ์ดังกล่าวเกิดขึ้นด้วยความน่าจะเป็นไม่เกิน $\delta$ เราสามารถกำหนดให้

$2\left(\frac{2em}{d}\right)^d2^{-\epsilon m/2}\leq\delta$

ซึ่งจะทำให้เราได้ hypothesis ตามต้องการด้วยความน่าจะเป็นอย่างน้อย $1-\delta$ เมื่อมีจำนวนตัวอย่างข้อมูลเป็น

$m\geq \frac{2}{\epsilon}\left(d\log\frac{2em}{d}+\log\frac{2}{\delta}\right)$

เพื่อความชัดเจน เราจะใช้ $\log$ แทนฟังก์ชัน logarithm ฐาน 2 และใช้ $\ln$ แทน natural logarithm หรือ logarithm ฐาน $e$

สังเกตว่าอสมการด้านบนนี้ยังไม่สามารถบอกจำนวนข้อมูลที่ต้องการแก่เราได้ เนื่องจากสูตรด้านขวามือยังคงมีตัวแปร $m$ ติดอยู่ ดังนั้นเราจึงต้องพยายามหาขอบเขตของ $m$ ใหม่ให้ ขึ้นอยู่กับ $\epsilon, \delta,$ และ $d$ หากเราพิจารณาค่าของ $m$ ที่น้อยที่สุดที่สอดคล้องกับเงื่อนไขดังกล่าว นั่นคือเราพิจารณา $m$ ที่

$\begin{split} m&= \frac{2}{\epsilon}\left(d\log\frac{2em}{d}+\log\frac{2}{\delta}\right)\\ &=\frac{2}{\epsilon}\left(d\log m+d\log\frac{2e}{d}+\log\frac{2}{\delta}\right)\\ &=\frac{2d}{\epsilon}\log m+\frac{2}{\epsilon}\left(d\log\frac{2e}{d}+\log\frac{2}{\delta}\right) \end{split}$

คราวนี้เราจะจำกัดขอบเขตของค่า $\log m$ ดังนี้ พิจารณาฟังก์ชัน $y_1=\log x$ และฟังก์ชันเส้นตรง $y_2=ax+b$ ที่แตะกันที่จุด $x=\alpha$ ดังรูป

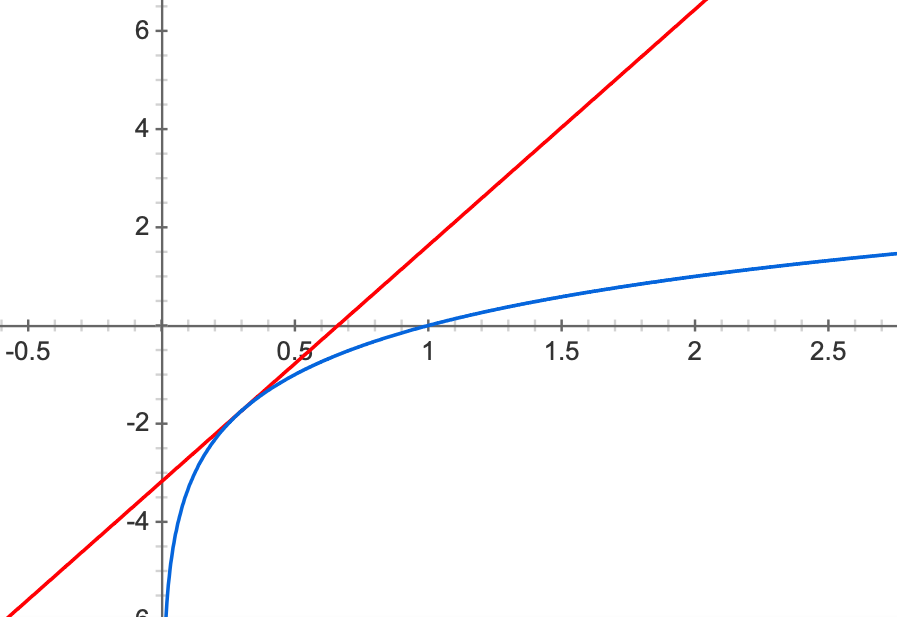
เนื่องจากที่จุด $x=\alpha$ ความชันของทั้งสองเส้นต้องเท่ากัน นั่นคือ

$a = \left.\frac{\text{d}}{\text{d} x}\log x\right|_\alpha = \left.\frac{1}{x\ln 2}\right|_\alpha = \frac{1}{\alpha\ln2}$

และที่จุดนี้ ค่าของ $y_1$ และ $y_2$ ต้องเท่ากันด้วย เราจึงได้ว่า

$\log\alpha = \frac{1}{\alpha\ln2}\alpha + b$

ดังนั้น

$b=\log\alpha -\frac{1}{\ln2}$

เนื่องจากฟังก์ชันเส้นตรง $y_2$ นั้นเป็นขอบเขตบนให้กับ $y_1$ เสมอ เราจึงได้ว่า สำหรับ $\alpha>0$

$\log x\leq \frac{1}{\alpha\ln2}x+\log\alpha -\frac{1}{\ln2}$

ดังนั้นหากเราแทน $x$ ด้วย $m$ และแทน $\alpha$ ด้วย $\frac{4d}{\epsilon\ln2}$ ในสมการด้านบน เราจะได้ว่า

$\begin{split} m&\leq \frac{2d}{\epsilon}\left(\frac{\epsilon}{4d}m+\log\frac{4d}{\epsilon\ln2}-\frac{1}{\ln2}\right)+\frac{2}{\epsilon}\left(d\log\frac{2e}{d}+\log\frac{2}{\delta}\right)\\ &=\frac{m}{2}+\frac{2}{\epsilon}\left(d\log\frac{4d}{\epsilon\ln2}-\frac{d}{\ln2}+d\log\frac{2e}{d}+\log\frac{2}{\delta}\right) \end{split}$

เนื่องจาก $\frac{d}{\ln2}$ จัดรูปได้เป็น $\frac{d\log e}{\log 2}=d\log e$ ดังนั้นเราจึงได้ว่า

$\begin{split} \frac{m}{2}&\leq\frac{2}{\epsilon}\left(d\log\left(\frac{4d}{\epsilon\ln2}\cdot\frac{1}{e}\cdot\frac{2e}{d}\right)+\log\frac{2}{\delta} \right)\\ \end{split}$

หรือได้เป็น

$\begin{split} m&\leq\frac{4}{\epsilon}\left(d\log\frac{8}{\epsilon\ln2}+\log\frac{2}{\delta}\right)\\ &\leq\frac{4}{\epsilon}\left(d\log\frac{12}{\epsilon}+\log\frac{2}{\delta}\right) \end{split}$

ดังนั้นเราสรุปได้ว่า หากเรามีตัวอย่างข้อมูลจำนวน $m$ ตัวเมื่อ

$m\geq \frac{4}{\epsilon}\left(d\log\frac{12}{\epsilon}+\log\frac{2}{\delta}\right)$

เราจะรับประกันได้ว่า ด้วยความน่าจะเป็นไม่น้อยกว่า $1-\delta$ hypothesis $h$ ของเราที่ consistent กับตัวอย่างข้อมูลทั้งหมดจะมี risk $R(h)$ ไม่เกิน $\epsilon$ เราอาจกล่าวได้ว่าการเรียนรู้ของเรามี sample complexity เป็น $O(\frac{1}{\epsilon}(d\log\frac{1}{\epsilon}+\log\frac{1}{\delta}))$

inconsistent hypothesis

สำหรับกรณีที่ hypothesis $h$ ไม่ได้ consistent กับตัวอย่างข้อมูลใน $S$ ทั้งหมด เราสามารถใช้เทคนิคการวิเคราะห์แบบเดียวกันสรุปได้ว่า ด้วยความน่าจะเป็นไม่น้อยกว่า $1-\delta$ เราจะได้ $R(h)\leq \hat{R}_S(h)+\epsilon$ เมื่อเรามีจำนวนตัวอย่างข้อมูล $m$ ตัวโดยที่

$m\geq\frac{64}{\epsilon^2}\left(2d\ln\frac{12}{\epsilon}+\ln\frac{4}{\delta}\right)$

หรือเรากล่าวได้ว่ามี sample complexity เป็น $O(\frac{1}{\epsilon^2}(d\log\frac{1}{\epsilon}+\log\frac{1}{\delta}))$

Computational-Learning-Theory

ทฤษฎีการเรียนรู้เชิงคำนวณ

Sample complexity

inconsistent hypothesis