VC-Dimension
จากหัวข้อที่แล้ว จะเห็นว่าหากกำหนดจำนวนของตัวอย่างข้อมูลมาให้เท่ากับ $m$ เราสามารถพิจารณาพลังในการจำแนกข้อมูล $m$ ตัวของ hypothesis space $H$ ใด ๆ ได้จากค่าของ growth function $\Pi_H(m)$ โดย hypothesis space $H$ ที่มีอัตราการโตของ $\Pi_H(m)$ สูงก็จะมีความซับซ้อนสูง หรือมีพลังในการจำแนกข้อมูลสูงกว่า hypothesis space $H$ ที่มีอัตราการโตของ $\Pi_H(m)$ นั่นเอง
ในหัวข้อนี้เราจะมาทำความรู้จักกับ VC-dimension (Vapnik-Chervonenkis dimension) ซึ่งเป็นปริมาณเชิง combinatorial ที่มีความสัมพันธ์กับ growth function เป็นอย่างมาก และสามารถใช้บอกความซับซ้อนของ hypothesis space ต่าง ๆ ได้เช่นกันไม่ว่า hypothesis space นั้นจะมีขนาดจำกัดหรือไม่ เราจะได้เห็นต่อไปว่า VC-dimension นี้มีบทบาทอย่างมากจนถือได้ว่าเป็นหนึ่งในหัวใจสำคัญของทฤษฎีการเรียนรู้เชิงคำนวณ
ในการนิยาม VC-dimension ของ hypothesis space $H$ เราจะทบทวนเกี่ยวกับ dichotomy และการ shatter กันก่อน สำหรับ hypothesis space $H$ ใด ๆ dichotomy ของ $H$ บนตัวอย่างข้อมูล คือวิธีการที่เป็นไปได้ในการ label $x_i$ แต่ละตัวด้วย hypothesis ที่อยู่ใน $H$ ถ้าหากสำหรับการ label $x_i$ ทั้ง $2^m$ แบบนั้น มี hypothesis ใน $H$ ที่ให้ label สอดคล้องทั้งหมด เราจะกล่าวว่า $H$ shatter
นิยาม VC-dimension ของ hypothesis space $H$ คือขนาดของเซตตัวอย่างข้อมูล $S$ ที่ใหญ่ที่สุดที่ถูก shatter ได้โดย $H$ นั่นคือ ถ้าให้ $d_H$ แทน VC-dimension ของ $H$
จากนิยามแสดงว่าจะต้องมีเซต $S$ ของตัวอย่างข้อมูลจำนวน $d_H$ อย่างน้อยเซตหนึ่งที่ $H$ shatter $S$ และหากพิจารณาเซตของตัวอย่างข้อมูลจำนวน $d_H+1$ ตัวขึ้นไป ไม่ว่าจะเป็นเซตใดก็จะไม่มีทางถูก shatter โดย $H$ ได้ ดังนั้น เราอาจนิยาม VC-dimension $d_H$ ในอีกมุมหนึ่งได้เป็นค่า $m$ ที่มากที่สุดที่มี growth function เท่ากับ $2^m$ นั่นเอง หรือเขียนได้เป็น
และถ้าสำหรับ $m\geq 0$ ใด ๆ $\Pi_H(m)=2^m$ เสมอ เราจะกล่าวว่า $d_H=\infty$
ในการแสดงว่า VC-dimension ของ $H$ มีค่าเท่ากับ $d$ นั้น เราทำได้โดยแสดงให้เห็นว่ามีเซตของตัวอย่างข้อมูล $d$ ตัวอย่างน้อยชุดหนึ่ง ที่ถูก shatter ได้จาก $H$ (นั่นคือ แสดงว่า $d_H\geq d$) และแสดงให้เห็นว่าสำหรับตัวอย่างข้อมูลใด ๆ ที่มีจำนวน $d+1$ ตัวจะไม่สามารถถูก shatter จาก $H$ ได้เลย (นั่นคือ แสดงว่า $d_H<d$)
ต่อจากนี้เราลองมาดูการวิเคราะห์ VC-dimension ของตัวอย่าง hypothesis space ง่าย ๆ จำนวนหนึ่งเพื่อให้เข้าใจมากขึ้น
Positive rays
ในกรณีของ $H$ ที่เป็นเซตของ positive rays สังเกตว่าสำหรับตัวอย่างข้อมูลเพียงจุดเดียว เราสามารถสร้าง hypothesis $h$ ที่ทำให้ตัวอย่างข้อมูลดังกล่าวมี label เป็น 1 หรือ 0 ก็ได้ดังรูปต่อไปนี้ แสดงว่า VC-dimension ของ positive rays มีค่าไม่น้อยกว่า 1 หรือ $d_H\geq 1$
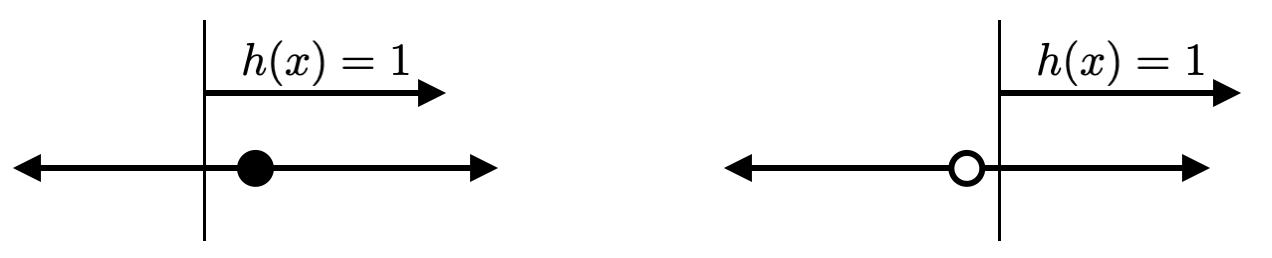
สำหรับตัวอย่างข้อมูลที่มีสองจุด $x_1$ และ $x_2$ ถ้า $x_1=x_2$ เราจะได้ว่า label ของทั้งสองจุดนี้จะต้องเหมือนกันเสมอ นั่นทำให้ dichotomy ที่สองจุดนี้มี label ต่างกันไม่สามารถเกิดขึ้นได้ แสดงว่า $H$ ไม่ shatter เซตของจุดทั้งคู่นี้ สำหรับกรณีที่ $x_1\neq x_2$ สมมติให้ $x_1<x_2$ จะเห็นว่าเราไม่สามารถ หา positive rays ที่ทำให้ได้ label ของ $x_1$ เป็น 1 และ label ของ $x_2$ เป็น 0 ได้เลย (แสดงตามรูปด้านล่าง) ดังนั้น $H$ ก็ไม่ shatter เซตของจุดทั้งคู่นี้เช่นกัน จากตรงนี้จะเห็นว่าเซตของตัวอย่างข้อมูลจำนวนสองจุดใด ๆ ไม่มีทางถูก shatter จาก $H$ ได้เลย นั่นแสดงว่า $d_H<2$
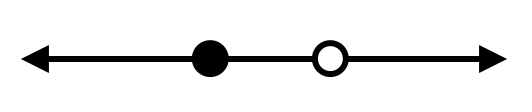
เนื่องจาก $d_H\geq 1$ และ $d_H<2$ เราจึงได้ว่าเมื่อ $H$ เป็นเซตของ positive rays $H$ จะมี VC-dimension เป็น $d_H=1$
Positive Intervals
ในกรณีของ $H$ ที่เป็นเซตของ positive intervals นั้นจะเห็นว่าไม่มีปัญหาในการสร้าง dichotomy ให้ครบทุกแบบสำหรับตัวอย่างข้อมูลสองตัว โดยตัวอย่างของ hypothesis ที่ทำให้ได้ dichotomy แต่ละแบบแสดงในรูปด้านล่างนี้ จากตรงนี้เราจึงได้ว่า VC-dimension ของ $H$ มีค่าเป็น $d_H\geq 2$
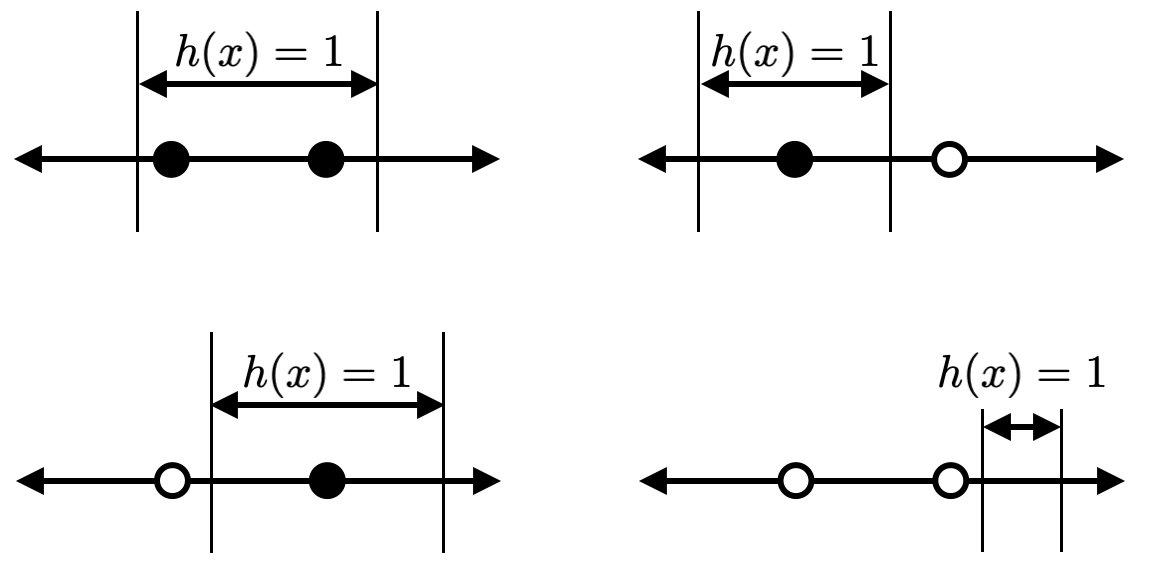
สำหรับตัวอย่างข้อมูลสามตัว ถ้าไม่มีตัวอย่างข้อมูลที่ซ้ำกันเลย เราจะได้ว่า dichotomy ที่แสดงในรูปด้านล่างนี้ไม่สามารถสร้างได้จาก hypothesis ใด ๆ ใน $H$ ดังนั้นเราจึงได้ว่า $d_H<3$ ซึ่งทำให้เราสรุปได้ว่า VC-dimension ของเซตของ positive intervals จะมีค่าเท่ากับ 2 ซึ่งมากกว่า VC-dimension ของ positive rays นั่นแสดงให้เห็นว่า positive intervals นั้นมีพลังในการจำแนกข้อมูลมากกว่านั่นเอง

Convex Sets
ในกรณีของ $H$ ที่เป็นเซตของ convex set บนระนาบสองมิติ จากหัวข้อที่แล้วเราได้วิเคราะห์กันแล้วว่าไม่ว่าจำนวนตัวอย่างข้อมูล $m$ จะเป็นเท่าไหร่ก็ตาม เราสามารถหาเซตของตัวอย่างข้อมูล $m$ ตัวที่ทำให้ $\Pi_H(m)=2^m$ ได้เสมอ นั่นแสดงว่ามีเซต $S$ ของตัวอย่างข้อมูล $m$ ตัวที่ $H$ สามารถ shatter $S$ ได้ไม่ว่า $m$ จะมีค่าเท่าไหร่ จากนิยาม เราจึงได้ว่า VC-dimension ของ $H$ ในกรณีนี้มีค่าเป็น $\infty$ นั่นเอง
รูปสี่เหลี่ยมขนานแกน
ย้อนกลับมาดู hypothesis space $H$ ที่เป็นเซตของรูปสี่เหลี่ยมขนานแกนบนระนาบสองมิติ เมื่อ $X=\mathbb{R}^2$ เราสามารถแสดงได้ว่า VC-dimension มีค่าไม่น้อยกว่า 4 โดยพิจารณาตัวอย่างข้อมูลสี่จุดที่อยู่ในตำแหน่งดังรูปต่อไปนี้ จะเห็นว่าไม่ว่าเราจะกำหนด label ของแต่ละจุดเป็นแบบใด ก็จะสามารถหารูปสี่เหลี่ยมขนานแกนที่สอดคล้องกับ label ดังกล่าวได้เสมอ ในรูปแสดงตัวอย่างรูปสี่เหลี่ยมขนานแกนที่ทำให้ label ของจุดบนและจุดล่างเป็น 1 และอีกสองจุดเป็น 0
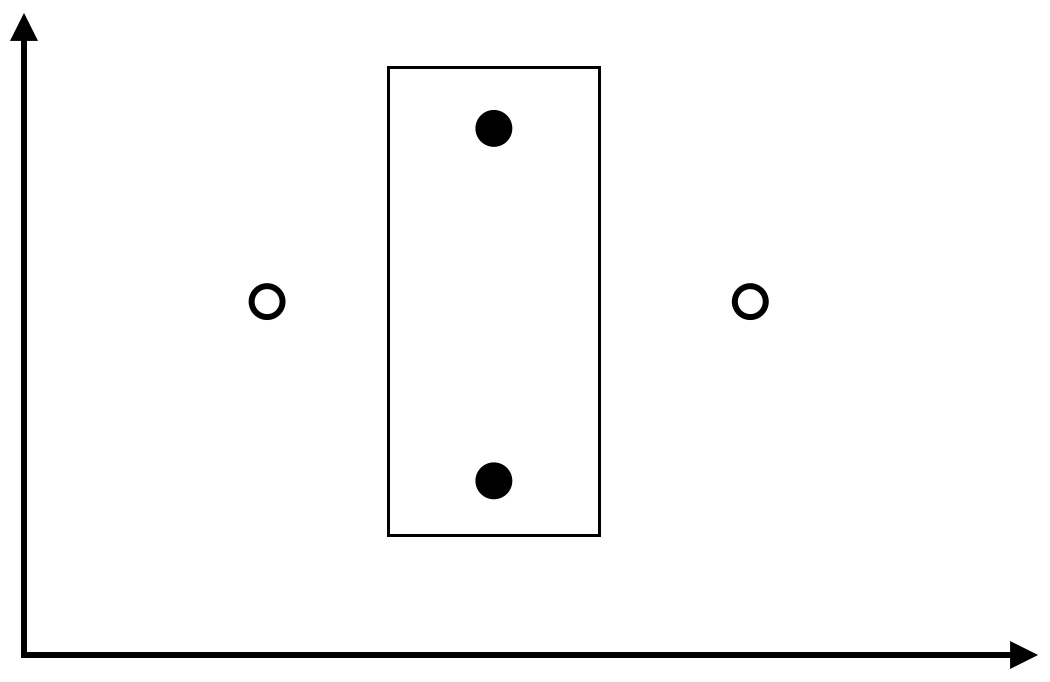
ในขณะที่ถ้าเราพิจารณาเซตของตัวอย่างข้อมูล 5 ตัวใด ๆ จะต้องมีอย่างน้อยหนึ่งตัวที่ไม่ได้เป็นทั้งจุดที่อยู่บนสุด ล่างสุด ซ้ายสุด หรือขวาสุด ซึ่งถ้าเราพิจารณาการ label ตัวอย่างข้อมูลที่ให้จุดดังกล่าวมี label เป็น 0 และจุดที่เหลือมี label เป็น 1 หมด (เช่นในรูปด้านล่าง) จะเห็นว่าเราไม่สามารถสร้างรูปสี่เหลี่ยมขนานแกนให้ครอบคลุมจุดทั้งสี่แต่ไม่ครอบคลุมจุดภายในได้ นั่นแสดงว่า VC-dimension จะต้องมีค่าน้อยกว่า 5 แน่นอน
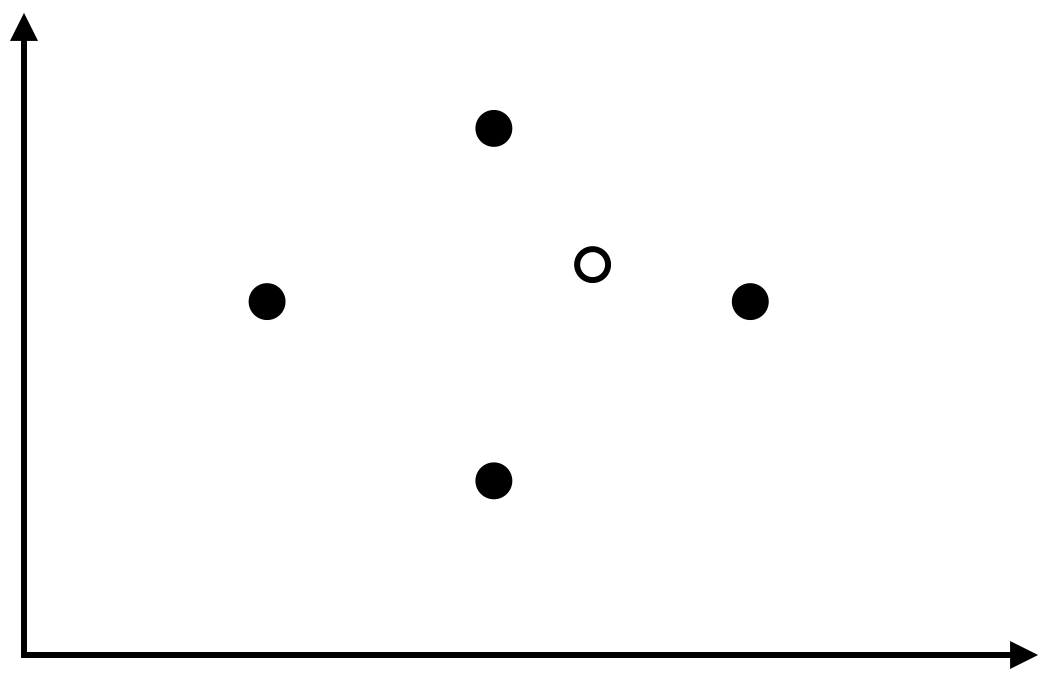
เราจึงสามารถสรุปได้ว่า VC-dimension ของรูปสี่เหลี่ยมขนานแกนมีค่าเท่ากับ 4
Hyperplanes
พิจารณา $H$ ที่เป็นเซตของ linear classifier บน $\mathbb{R}^2$ สังเกตว่าสำหรับเซต $S$ ของจุดบนระนาบสามจุดใด ๆ ที่ไม่ได้เรียงอยู่ในแนวเส้นตรงเดียวกัน $H$ จะ shatter $S$ เสมอ รูปด้านล่างแสดงตัวอย่าง linear classifier ที่สอดคล้องกับ label ของจุดทั้งสาม นั่นแสดงว่า VC-dimension มีค่าไม่น้อยกว่า 3
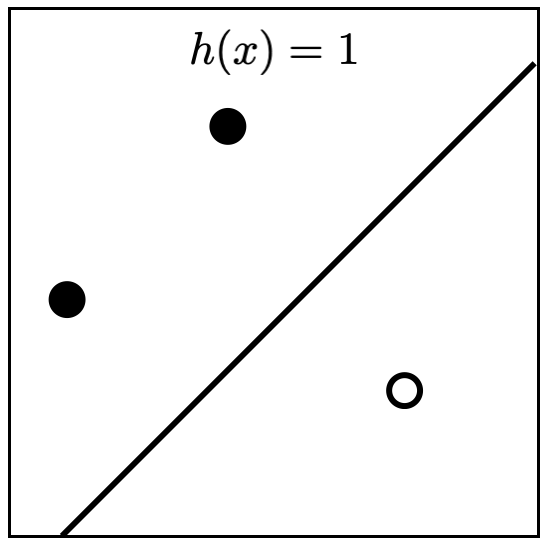
สำหรับ $S$ ที่เป็นเซตของจุดจำนวนสี่จุด เราจะแบ่งการพิจารณาเป็นสองกรณีดังนี้
- เมื่อรูป convex hull ของจุดทั้งสี่เป็นรูปสี่เหลี่ยมที่มีสี่จุดดังกล่าวเป็นจุดมุม จะเห็นว่าหากเรากำหนด label ให้จุดที่อยู่ในแนวทะแยงมี label เหมือนกัน เช่นในรูปย่อยด้านซ้ายของรูปต่อไปนี้ จะเห็นว่าเราจะไม่สามารถหา linear classifier ที่สอดคล้องกับ label ดังกล่าวได้เลย
- เมื่อรูป convex hull ของจุดทั้งสี่เป็นรูปสามเหลี่ยม และมีจุดหนึ่งอยู่ภายในสามเหลี่ยมนั้น เราจะได้ว่าหากเรากำหนด label ของจุดภายในให้แตกต่างกับสามจุดที่เหลือเช่นในรูปย่อยด้านขวา ก็จะไม่สามารถหา linear classifier ที่สอดคล้องกับ label ดังกล่าวได้เช่นกัน
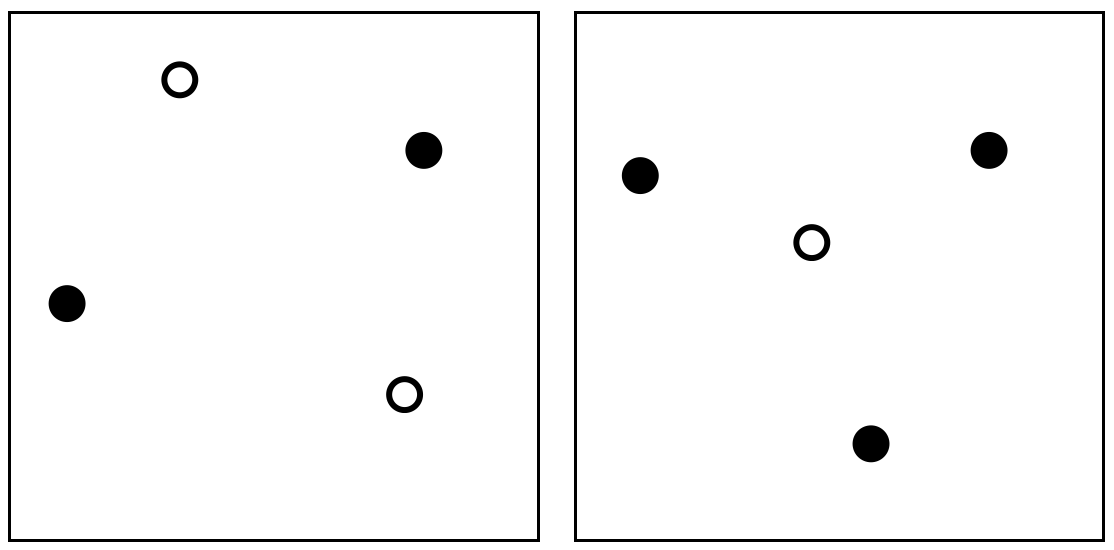
จากการพิจารณาทั้งสองกรณี จะเห็นว่าสำหรับ $S$ ที่เป็นเซตของตัวอย่างข้อมูลสี่จุดใด ๆ $H$ ของเราไม่สามารถ shatter $S$ ได้เลย นั่นแสดงว่า VC-dimension ของ $H$ จะต้องมีค่าน้อยกว่า 4 นั่นเอง เราจึงสรุปได้ว่า VC-dimension ของ linear classifier บนระนาบ $\mathbb{R}^2$ มีค่าเป็น 3
ในกรณีทั่วไป เราสามารถแสดงให้เห็นได้ว่า VC-dimension ของ hyperplanes บน $\mathbb{R}^d$ จะมีค่าเท่ากับ $d+1$
Prev: Growth Function