ปัญหาที่เรียนรู้ยาก
ในหัวข้อนี้ เราจะมาดูตัวอย่าง concept class หนึ่ง ซึ่งสามารถพิสูจน์ได้ว่าการเรียนรู้ concept class ดังกล่าวนี้ไม่สามารถทำได้อย่างมีประสิทธิภาพ นอกจากทุกปัญหาในคลาส NP สามารถหาคำตอบได้อย่างมีประสิทธิภาพด้วยความมั่นใจสูง
ปัญหาการเรียนรู้ 3-term DNF
ปัญหาที่เราสนใจในหัวข้อนี้ เป็นปัญหาการเรียนรู้ concept ที่เป็น boolean formula ที่ซับซ้อนขึ้นกว่า boolean conjunction เล็กน้อย กล่าวคือ boolean formula ที่เราสนใจจะเรียนรู้ในหัวข้อนี้จะอยู่ในรูป disjunctive normal form (DNF) ที่มี 3 term ซึ่งคือรูปแบบของ conjunction จำนวนสามกลุ่มมาดำเนินการ logical or เข้าด้วยกัน เราจะเรียกปัญหาการเรียนรู้นี้ว่า ปัญหาการเรียนรู้ 3-term DNF โดยที่ concept class $C$ ของเราจะเป็นเซตของ disjunction ในรูป
เมื่อแต่ละ $T_i$ เป็น boolean conjunction บน literal ของตัวแประ $x_1,\dots,x_n$ สังเกตว่าเราสามารถนิยามขนาดของ representation ของ 3-term DNF $c\in C$ ได้ด้วยผลบวกของจำนวน literal ที่ปรากฏในแต่ละ $T_i$ ซึ่งจะมีค่าไม่เกิน $6n$ (เนื่องจากแต่ละ $T_i$ มี literal ได้ไม่เกิน $2n$ ตัว) ดังนั้นเราจึงได้ว่า $size(c)\leq 6n$ สำหรับทุก concept $c\in C$ นั่นหมายความว่าอัลกอริทึมการเรียนรู้ที่มีประสิทธิภาพ จะต้องใช้เวลาทำงานเป็น polynomial บน $1/\epsilon, 1/\delta$ และ $n$
เพื่อที่จะแสดงว่าปัญหา 3-term DNF นี้เรียนรู้ได้ยาก เราจะมาทำความเข้าใจความรู้พื้นฐานเพิ่มเติมก่อนเล็กน้อย
กลุ่มปัญหา RP
สำหรับปัญหาการตัดสินใจ (decision problem) $X$ ใด ๆ เราจะกล่าวว่า $X\in RP$ หรือ $X$ อยู่ในกลุ่มปัญหา RP ถ้ามีอัลกอริทึมเชิงสุ่ม $A$ ที่ทำงานภายในเวลาที่เป็น polynomial บนขนาดของ input และ
- สำหรับ input $a$ ที่มีคำตอบที่ถูกต้องเป็น NO เราจะได้ว่า $A(a)$ จะให้คำตอบเป็น NO
- สำหรับ input $a$ ที่มีคำตอบที่ถูกต้องเป็น YES เราจะได้ว่า $A(a)$ จะให้คำตอบเป็น YES ด้วยความน่าจะเป็นไม่น้อยกว่า $1/2$
เนื่องจาก $A$ เป็นอัลกอริทึมเชิงสุ่ม จึงทำให้การทำงานของ $A$ บน input $a$ ตัวเดียวกันในแต่ละครั้งอาจได้ผลแตกต่างกัน จากเงื่อนไขของ $A$ จะเห็นว่า เมื่อใดก็ตามที่เราเรียก $A$ ให้ทำงานบน input $a$ ตัวหนึ่งแล้วได้ผลเป็น YES แสดงว่า input $a$ ตัวนั้นจะต้องมีคำตอบที่ถูกต้องเป็น YES อย่างแน่นอน ในขณะที่หากได้ผลเป็น NO เราไม่สามารถสรุปอย่างชัดเจนได้ว่าคำตอบที่ถูกต้องเป็นเช่นไร
สังเกตว่าหากเรามีอัลกอริทึม $A$ ที่มีคุณสมบัติดังกล่าว สำหรับ input $a$ ที่มีคำตอบที่ถูกต้องเป็น YES ถ้าเราเรียกให้ $A$ ทำงานบน $a$ ซ้ำกันเป็นจำนวน $n$ ครั้ง (โดยการทำงานในแต่ละครั้งเป็นอิสระจากกัน) เราจะได้ว่าความน่าจะเป็นที่เราไม่พบคำตอบเป็น YES เลยแม้แต่ครั้งเดียวจะมีค่าไม่เกิน $1/2^n$ เราสามารถใช้แนวคิดนี้ในการปรับปรุงอัลกอริทึมให้มีความน่าจะเป็นที่จะตอบถูกต้องสูงตามต้องการได้
ในปัจจุบันเราทราบว่ากลุ่มปัญหา RP นั้นครอบคลุมปัญหาทั้งหมดในกลุ่ม P และเป็นสับเซตของกลุ่มปัญหา NP แต่ไม่ทราบว่า RP$=$NP หรือไม่
การลดรูปปัญหา
แนวคิดหลักในการแสดงว่าปัญหา 3-term DNF นั้นเรียนรู้ได้ยาก คือการแสดงให้เห็นว่ามีปัญหาในกลุ่ม NP-complete บางปัญหาที่สามารถลดรูปมาเป็นปัญหาการเรียนรู้ 3-term DNF ได้ กล่าวคือ เราจะแสดงกระบวนการแปลง input $a$ ใด ๆ ของปัญหา NP-complete นั้นให้กลายเป็นเซตของตัวอย่างข้อมูล $S_a$ สำหรับปัญหา 3-term DNF โดยที่ขนาดของ $S_a$ นั้นเป็น polynomial บนขนาดของ $a$ และแสดงให้เห็นว่า ถ้าเรามีอัลกอริทึมการเรียนรู้ $L$ ที่สามารถเรียนรู้ปัญหา 3-term DNF ตามกรอบการเรียนรู้แบบ PAC ได้ เราจะสามารถนำผลการเรียนรู้นั้นไปคำนวณต่อเพื่อหาคำตอบที่ถูกต้องของ input $a$ ในปัญหาตั้งต้นได้ ซึ่งจะนำไปสู่ข้อสรุปที่ว่ามีปัญหา NP-complete ที่สามารถหาคำตอบที่ถูกต้องด้วยความมั่นใจสูงได้อย่างมีประสิทธิภาพ หรือแสดงว่า RP=NP นั่นเอง
consistent hypothesis
หัวใจหลักของการลดรูปปัญหาของเราก็คือ เราจะทำการแปลง input $a$ ของปัญหาต้นทางมาเป็นเซตของตัวอย่างข้อมูล $S_a$ โดยมีเงื่อนไขว่า คำตอบที่ถูกต้องของ $a$ ในปัญหาตั้งต้นนั้นจะเป็น YES ก็ต่อเมื่อตัวอย่างข้อมูล $S_a$ ที่ได้มานั้นจะต้อง สอดคล้อง (consistent) กับ concept $c$ อย่างน้อยหนึ่งตัวใน $C$ โดยเรานิยามความสอดคล้องดังนี้
ให้ เป็นเซตของตัวอย่างข้อมูลโดย $x_i\in X$ และ สำหรับค่า $i=1,\dots,m$ ให้ $c$ เป็น concept ใด ๆ บน input space $X$ เราจะกล่าวว่า $c$ สอดคล้องกับ $S$ ถ้า $c(a_i)=y_i$ สำหรับทุกค่า $i=1,\dots,m$
ถ้า concept class $C$ นั่นสามารถเรียนรู้ได้อย่างมีประสิทธิภาพ เราจะสามารถตรวจสอบได้ด้วยความมั่นใจสูงว่ามี concept $c\in C$ ที่สอดคล้องกับเซตของตัวอย่างข้อมูล หรือไม่ โดยเรากำหนดการกระจายตัวให้มีความน่าจะเป็นที่ข้อมูล $(x_i,y_i)$ แต่ละคู่จะถูกเลือกมีค่าเป็น $1/m$ เท่ากันทั้งหมด และกำหนดค่า error parameter $\epsilon = 1/2m$ จากนั้นเรียกอัลกอริทึมการเรียนรู้ให้ทำงาน ด้วยวิธีการนี้ สังเกตว่าถ้าใน $C$ มี concept $c$ อย่างน้อยหนึ่งตัวที่สอดคล้องกับ $S$ อัลกอริทึมการเรียนรู้จะให้ผลเป็น $c\in C$ ที่สอดคล้องกับ $S$ ด้วยความน่าจะเป็นไม่ต่ำกว่า $1-\delta$ เนื่องจากถ้ามีตัวอย่างข้อมูลใน $S$ สักตัวที่ hypothesis $h$ ที่ได้จากการเรียนรู้ตอบผิด ค่า error $R(h)$ จะมีค่าอย่างน้อย $1/m=2\epsilon>\epsilon$ ในทางกลับกัน หากใน $C$ ไม่มี concept ใดเลยที่สอดคล้องกับ $S$ อัลกอริทึมการเรียนรู้ของเราก็จะไม่สามารถหา concept ที่สอดคล้องมาได้แน่นอน จากตรงนี้จะเห็นว่า หาก $C$ สามารถเรียนรู้ได้อย่างมีประสิทธิภาพ ปัญหาการตรวจสอบความสอดคล้องของเซต $S$ กับ $C$ นี้จะอยู่ในกลุ่มปัญหา RP ดังนั้น หากเราสามารถลดรูปปัญหา NP-complete ให้กลายมาเป็นปัญหาการตรวจสอบความสอดคล้องเช่นนี้ได้ จากสมมติฐานที่ว่า RP$\neq$NP เราก็จะสรุปได้ว่าอัลกอริทึมการเรียนรู้ $C$ ที่มีประสิทธิภาพนั้นจะมีอยู่จริงไม่ได้
การลดรูปจากปัญหาการระบายสามสีบนกราฟ
ถึงตรงนี้ สิ่งที่เหลือในการแสดงว่าปัญหาการเรียนรู้ 3-term DNF นั้นเป็นปัญหาที่ยาก ก็คือการแสดงให้เห็นว่ามีปัญหา NP-complete ที่สามารถลดรูปมาเป็นปัญหาการตรวจสอบความสอดคล้องของ 3-term DNF ได้ ปัญหาที่เราจะใช้แสดงการลดรูปนี้ก็คือปัญหา การระบายสามสีบนกราฟ หรือ Graph 3-Coloring ซึ่งมีนิยามดังนี้
ปัญหาการระบายสามสีบนกราฟ ให้กราฟแบบไม่มีทิศทาง $G=(V,E)$ โดย และ ต้องการตรวจสอบว่าเราสามารถระบายสีลงบนจุดยอดแต่ละจุดใน $V$ โดยใช้สีไม่เกิน 3 สีและให้เส้นเชื่อม $(i,j)\in E$ แต่ละเส้นมีสีที่จุดปลายทั้งสองด้านไม่เหมือนกันได้หรือไม่
เราจะแปลง input ของปัญหาจากกราฟ $G=(V,E)$ มาเป็นเซตของตัวอย่างข้อมูล $S_G$ ดังนี้ สำหรับแต่ละจุดยอด $i\in V$ เราจะสร้าง positive example $(v(i), 1)$ โดยที่ $v(i)$ เป็น bit string ความยาวเท่ากับ $n$ ที่มีบิตที่ $i$ เป็น 0 และบิตอื่น ๆ เป็น 1 ทั้งหมด นอกจากนี้ สำหรับเส้นเชื่อม $(i,j)\in E$ แต่ละเส้น เราจะสร้าง negative example $(e(i,j), 0)$ โดย $e(i,j)$ มีบิตที่ $i$ และ $j$ เป็น 0 และบิตอื่น ๆ เป็น 1 ทั้งหมด ตัวอย่างเช่น กราฟต่อไปนี้จะสามารถนำมาสร้างตัวอย่างข้อมูลได้ตามตารางด้านล่าง
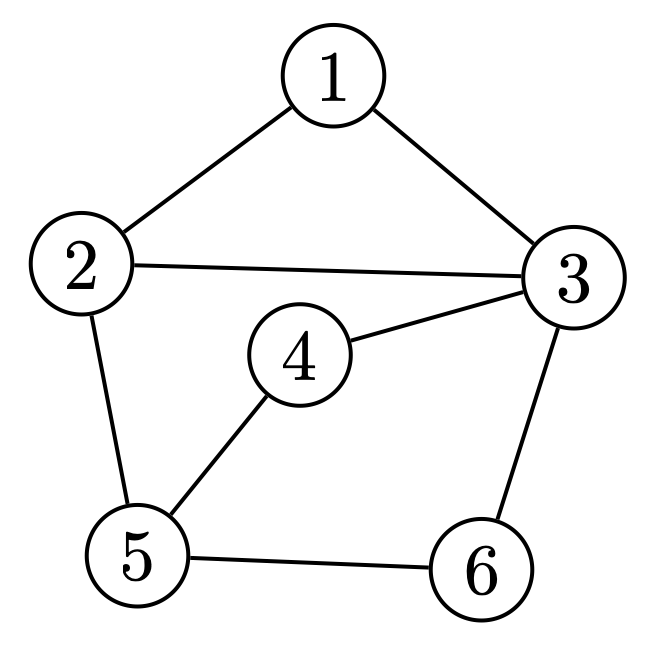
| example | label | example | label |
|---|---|---|---|
| $(0,1,1,1,1,1)$ | 1 | $(0,0,1,1,1,1)$ | 0 |
| $(1,0,1,1,1,1)$ | 1 | $(0,1,0,1,1,1)$ | 0 |
| $(1,1,0,1,1,1)$ | 1 | $(1,0,0,1,1,1)$ | 0 |
| $(1,1,1,0,1,1)$ | 1 | $(1,0,1,1,0,1)$ | 0 |
| $(1,1,1,1,0,1)$ | 1 | $(1,1,0,0,1,1)$ | 0 |
| $(1,1,1,1,1,0)$ | 1 | $(1,1,0,1,1,0)$ | 0 |
| $(1,1,1,0,0,1)$ | 0 | ||
| $(1,1,1,1,0,0)$ | 0 |
คราวนี้เราจะมาพิสูจน์กันว่า กราฟ $G$ จะสามารถระบายโดยใช้สามสีได้ก็ต่อเมื่อมี 3-term DNF ที่สอดคล้องกับ $S_G$ ขั้นแรก ถ้ากราฟ $G$ สามารถระบายโดยใช้สามสีได้ สมมติให้ $R,B,Y$ เป็นเซตของจุดยอดใน $G$ ที่ระบายด้วยสีแดง น้ำเงิน และเหลือง ตามลำดับ ถ้าให้ $T_R$ เป็น conjunction ที่ประกอบด้วยตัวแปรในเซต จะเห็นว่า positive example $v(i)$ ที่สร้างจากจุดยอด $i\in R$ จะทำให้ $T_R$ เป็นจริงได้ เนื่องจากตัวแปรที่กำหนดเป็น 0 ไม่อยู่ใน $T_R$ สำหรับ negative example เราจะมั่นใจได้ว่าไม่มี negative example ใดที่สามารถทำให้ $T_R$ เป็นจริงได้ เนื่องจาก negative example $e(i,j)$ ใด ๆ จะกำหนดค่า 0 ให้กับ $x_i$ และ $x_j$ แต่ทั้ง $i$ และ $j$ ไม่สามารถระบายด้วยสีแดงทั้งคู่ได้ แสดงว่าจะต้องมี $x_i$ หรือ $x_j$ (หรือทั้งคู่) ที่ถูกกำหนดให้เป็น 0 และปรากฏอยู่ใน $T_R$ ซึ่งนำมาสู่ข้อขัดแย้ง
เมื่อเราวิเคราะห์เซต $B$ และ $Y$ ในลักษณะเดียวกัน ก็จะได้ว่า positive example แต่ละตัวจะทำให้ $T_R\lor T_B\lor T_Y$ เป็นจริงได้ ในขณะที่ไม่มี negative example ตัวใดทำให้เป็นจริงได้เลย นั่นคือ เราจะได้ว่ามี 3-term DNF $T_R\lor T_B\lor T_Y$ นี้ที่สอดคล้องกับ $S_G$ ภาพด้านล่างแสดงตัวอย่างการระบายสีบน $G$ และ conjunction $T_R,T_B,T_Y$
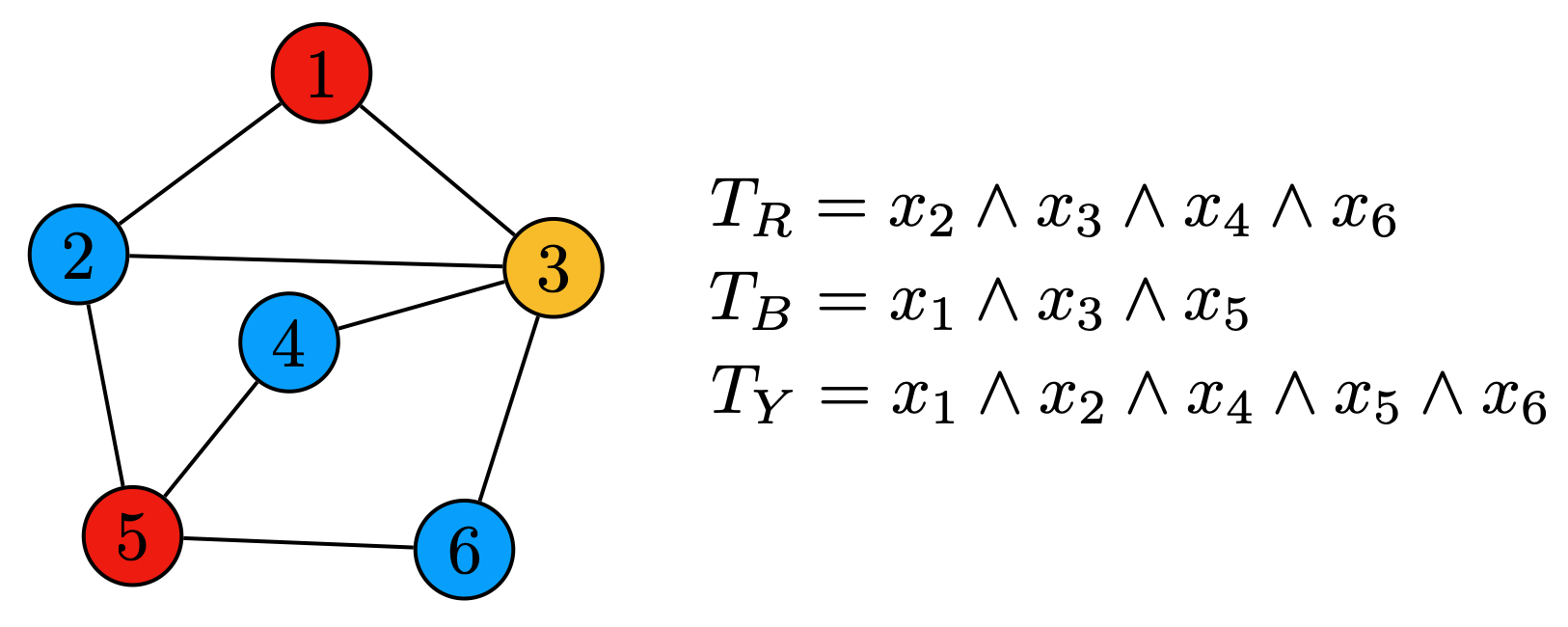
ในทางตรงข้าม สมมติให้มี 3-term DNF $T_1\lor T_2\lor T_3$ ที่สอดคล้องกับ $S_G$ เราจะแสดงการระบายสีจุดยอดใน $G$ เป็นสามสีดังนี้ ขั้นแรกดูว่า positive example $v(i)$ ตัวใดที่ทำให้ $T_1$ เป็นจริง เราจะระบายสีจุดยอด $i$ ด้วยสีแดง และลบ $v(i)$ ออกไป ในบรรดา positive example ที่เหลืออยู่ $v(i)$ ตัวใดทำให้ $T_2$ เป็นจริง เราจะระบายจุดยอด $i$ ด้วยสีน้ำเงิน และระบายสีจุดยอดที่เหลือด้วยสีเหลือง เนื่องจาก $T_1\lor T_2\lor T_3$ สอดคล้องกับ $S_G$ แสดงว่า positive example $v(i)$ แต่ละตัวจะต้องทำให้ conjunction อย่างน้อยตัวหนึ่งเป็นจริง แสดงว่าจุดยอดทั้งหมดจะต้องถูกระบายสีแน่นอน แต่จุดยอดที่มีเส้นเชื่อมถึงกันจะไม่สามารถมีสีเดียวกันได้ เนื่องจากถ้ามีเส้นเชื่อม $(i,j)\in E$ ที่ $i$ และ $j$ ถูกระบายด้วยสีเดียวกัน แสดงว่ามี conjunction $T_k$ ที่ $v(i)$ และ $v(j)$ ทำให้เป็นจริงได้ทั้งคู่ เนื่องจากบิตที่ $i$ ของ $v(i)$ เป็น 0 แต่บิตที่ $i$ ของ $v(j)$ เป็น 1 การที่ example ทั้งคู่จะทำให้ $T_k$ เป็นจริงแสดงว่าใน $T_k$ จะต้องไม่มี $x_i$ หรือ $\bar{x}_i$ อยู่เลย คราวนี้เนื่องจาก $v(j)$ และ $e(i,j)$ นั้นต่างกันที่บิตที่ $i$ เพียงบิตเดียว ถ้า $v(j)$ ทำให้ $T_k$ เป็นจริงได้ แสดงว่า $e(i,j)$ ก็ต้องทำให้ $T_k$ เป็นจริงได้เช่นกัน นั่นหมายความว่า 3-term DNF นี้จะต้องไม่สอดคล้องกับ $S_G$ เกิดเป็นข้อขัดแย้ง
ถึงตรงนี้เราจึงสรุปได้แล้วว่า ด้วยสมมติฐานว่า RP$\neq$NP เราจะไม่สามารถเรียนรู้ปัญหา 3-term DNF ได้อย่างมีประสิทธิภาพ