การปรับปรุงการเรียนรู้ Boolean Conjunction

จากหัวข้อที่แล้ว เราสามารถมองค่า

ว่าเป็นขนาดของพื้นที่ที่ต้องใช้ในการระบุถึง hypothesis แต่ละตัวใน $H$ (ในความเป็นจริง การระบุถึงสมาชิกใด ๆ ใน $H$ ต้องการพื้นที่ $\log_2 |H|$ ซึ่งแตกต่างจาก $\ln |H|$ ด้วยตัวประกอบที่เป็นค่าคงที่) จะเห็นว่า หากเราใช้พื้นที่ในการระบุ hypothesis น้อย แสดงว่าจำนวน hypothesis ที่สร้างได้จากอัลกอริทึมการเรียนรู้ยิ่งมีจำนวนน้อย และทำให้จำนวนตัวอย่างข้อมูลที่ต้องการในการเรียนรู้ตามกรอบของ PAC ก็จะน้อยตามไปด้วย ข้อสังเกตนี้สอดคล้องกับหลักการของออคแคมที่เรียกว่า Occam’s Razor ซึ่งถูกเสนอโดย William of Ockham โดยมีใจความสำคัญว่า

ถ้าเรามีทฤษฎีที่อธิบายปรากฏการณ์หนึ่งได้มากกว่าหนึ่งรูปแบบ ทฤษฎีที่มีเรียบง่ายที่สุดมักจะดีที่สุด

ในบริบทของอัลกอริทึมการเรียนรู้ของเรา เราอาจมองความเรียบง่ายหรือความซับซ้อนของอัลกอริทึมจากจำนวน hypothesis ที่แตกต่างกันทั้งหมดที่อัลกอริทึมนั้นสามารถสร้างได้ สังเกตว่าถ้าเราสามารถปรับปรุงอัลกอริทึมการเรียนรู้ของเราใหม่ ให้รับประกันได้ว่าจำนวน hypothesis ที่สร้างได้มีน้อยลง ก็จะนำไปสู่การเรียนรู้ที่มี sample complexity ที่ดีขึ้นกว่าเดิม

ในหัวข้อที่แล้ว เราสามารถทำการเรียนรู้ปัญหา Boolean Conjunction ได้โดยมี sample complexity เป็น $\frac{1}{\epsilon}(n\ln 3 +\ln\frac{1}{\delta})$ ซึ่งจะเห็นว่าขึ้นกับ $n$ แต่ไม่ขึ้นกับ $size(c)$ หรือขนาดของ representation จริงของ conjunction เป้าหมาย $c$ นั่นคือ ถึงแม้ว่า $c$ จะมีจำนวน literal น้อยกว่า $n$ เป็นอย่างมาก เราก็ยังต้องการจำนวนตัวอย่างข้อมูลในการเรียนรู้เท่าเดิม

ในหัวข้อนี้เราจะมาดูการปรับปรุงการเรียนรู้ปัญหา Boolean Conjunction นี้ใหม่ เพื่อใช้ในกรณีที่ $size(c)$ มีค่าน้อยกว่า $n$ เป็นอย่างมาก ($size(c)\ll n$) โดยในอัลกอริทึมใหม่นี้จะแตกต่างจากเดิมตรงที่เราจะนำ negative example มาพิจารณาด้วย อย่างไรก็ดี เราควรทำความเข้าใจว่าเวลาทำงานของอัลกอริทึมใหม่นั้นจำเป็นจะต้องขึ้นกับค่าของ $n$ อยู่ดี เนื่องจากตัวอย่างข้อมูลแต่ละตัวมีขนาดเป็น $n$ และอัลกอริทึมของเราจำเป็นจำต้องใช้เวลาให้เพียงพอเพื่ออ่านข้อมูลทั้งหมด

ก่อนที่จะไปดูอัลกอริทึมใหม่ เราจะมาทำความรู้จักปัญหาด้าน combinatorial ที่สำคัญมากปัญหาหนึ่งและอัลกอริทึมแบบประมาณสำหรับแก้ปัญหานี้ เพื่อจะนำไปประยุกต์ใช้กับอัลกอริทึมการเรียนรู้ใหม่ของเราต่อไป

ปัญหา Set Cover

ปัญหาที่เราจะพิจารณากันนี้ชื่อว่า ปัญหา Set Cover โดยมี input เป็นเซต $U=\{1,\dots, m\}$ และ $S=\{s_1,\dots,s_k\}$ โดยที่ $s_i\subseteq U$ สำหรับ $i=1\dots,k$ และ $s_1\cup\dots\cup s_k=U$ เราต้องการเลือกเซตใน $S$ จำนวนน้อยที่สุดที่ครอบคลุมสมาชิกทุกตัวใน $U$ หรือกล่าวคือ เราต้องการหา $T\subseteq S$ ที่มีขนาดน้อยที่สุดที่

ปัญหานี้เป็นหนึ่งในปัญหาที่มีชื่อเสียงที่สุดในกลุ่มปัญหา NP-complete ดังนั้นเราจึงไม่หวังว่าจะสามารถแก้ปัญหาได้ในเวลาที่เป็น polynomial บนขนาดของ input อย่างไรก็ดี เรามี อัลกอริทึมแบบประมาณ (approximation algorithm) โดยใช้แนวคิดแบบ greedy ที่สามารถรับประกันว่าหา set cover ได้โดยใช้จำนวนเซตไม่เกิน $\ln m$ เท่าของจำนวนเซตที่น้อยที่สุด นั่นคือ หากคำตอบที่ดีที่สุดใช้สมาชิกในเซต $S$ จำนวน $OPT$ ตัว อัลกอริทึมของเราจะให้คำตอบที่ครอบคลุมสมาชิกทุกตัวใน $U$ ได้โดยใช้จำนวนเซตไม่เกิน $(\ln m) OPT$ เราอาจกล่าวได้ว่าอัลกอริทึมนี้มี อัตราส่วนการประมาณ (approximation ratio) เป็น $\ln m$ นั่นเอง

อัลกอริทึมเริ่มจากการกำหนดค่าเริ่มต้นให้ $R=\emptyset$ จากนั้นเลือกเซต $s\in S$ ที่ครอบคลุมสมาชิกใน $U$ มากที่สุด เพิ่ม $s$ เข้าไปยัง $R$ และลบสมาชิกใน $s$ ออกจาก $U$ ทั้งหมด อัลกอริทึมจะวนรอบเลือกเซตใน $S\setminus R$ ที่ครอบคลุมสมาชิกที่เหลืออยู่ใน $U$ ให้มากที่สุด และเพิ่มเซตดังกล่าวเข้าไปยัง $R$ พร้อมกับลบสมาชิกที่ถูกครอบคลุมแล้วออกจาก $U$ เช่นนี้ไปเรื่อย ๆ จนกระทั่ง $U$ กลายเป็นเซตว่าง อัลกอริทึมก็จะคืน $R$ เป็นคำตอบ

ในการวิเคราะห์อัลกอริทึมนี้ ถ้าเราให้ $U_i$ แทนเซตของสมาชิกทั้งหมดใน $U$ ที่ยังไม่ถูกครอบคลุมหลังจากอัลกอริทึมทำการเลือกเซตไปแล้วจำนวน $i$ เซต โดยกำหนดให้ $U_0=U$

ในขั้นตอนแรก เมื่อสมาชิกที่ยังไม่ถูกครอบคลุมมีทั้งหมด $m$ ตัว เนื่องจากเราทราบว่า set cover ที่ดีที่สุดสามารถครอบคลุมสมาชิกทั้ง $m$ ตัวนี้ได้โดยใช้จำนวนเซตเป็น $OPT$ แสดงว่าจะต้องมีอย่างน้อยเซตหนึ่งที่ครอบคลุมสมาชิกใน $U_0$ เป็นจำนวนไม่น้อยกว่า $m/OPT$ (เนื่องจากถ้าทุกเซตครอบคลุมสมาชิกได้น้อยกว่า $m/OPT$ ทั้งหมด ต่อให้ไม่มีเซตคู่ใดมีส่วนที่ซ้อนทับกันเลย ก็จะครอบคลุมสมาชิกได้ทั้งสิ้นไม่ถึง $m$ ตัว) เนื่องจากอัลกอริทึมของเราเลือกเซตที่ครอบคลุมสมาชิกใน $U_0$ มากที่สุด ดังนั้นเราจึงรับประกันได้ว่าจำนวนสมาชิกที่ถูกครอบคลุมในขั้นตอนแรกนี้จะมีอย่างน้อย $m/OPT$ ตัว และจำนวนสมาชิกที่เหลืออยู่ใน $U$ หลังการเลือกเซตครั้งแรกนี้จะเป็น

เมื่อวิเคราะห์ในลักษณะเดียวกัน ในการเลือกเซตรอบที่ $i$ เราจะเลือกเซตที่ครอบคลุมสมาชิกใน $U_{i-1}$ มากที่สุด และเนื่องจาก $U_{i-1}\subseteq U$ ซึ่งสามารถครอบคลุมได้โดยใช้ไม่เกิน $OPT$ เซต เราจึงได้ว่าจะต้องมีอย่างน้อยเซตหนึ่งที่ครอบคลุมสมาชิกใน $U_{i-1}$ เป็นจำนวนไม่น้อยกว่า $|U_{i-1}|/OPT$ ดังนั้นเราก็จะได้ว่า

ซึ่งเราสามารถสรุปได้ว่า

หากเราต้องการหาจำนวนรอบที่ทำให้ครอบคลุมสมาชิกครบทุกตัวใน $U$ ก็ทำได้โดยกำหนดให้

ซึ่งก็จะได้ว่า

ดังนั้นจึงสรุปได้ว่า อัลกอริทึมของเรานี้จะสิ้นสุดการทำงานและให้คำตอบเป็น set cover ที่มีจำนวนเซตไม่เกิน $(\ln m) OPT$ หรือไม่เกิน $\ln m$ เท่าของคำตอบที่ดีที่สุดแน่นอน

อัลกอริทึมใหม่

คราวนี้เราจะแสดงอัลกอริทึมใหม่ในการเรียนรู้ปัญหา Boolean Conjunction ให้มีประสิทธิภาพในการเรียนรู้ดีขึ้นเมื่อ $size(c)\ll n$

อัลกอริทึมใหม่นี้จะเริ่มจากการทำงานแบบเดียวกับอัลกอริทึมเดิม นั่นคือเมื่อรับเซต $S$ ของตัวอย่างข้อมูลมาแล้ว อัลกอริทึมจะทำการตัด literal ทั้งหมดที่ขัดแย้งกับ positive example ออกไป ได้เป็น conjunction $h$ ที่สอดคล้องกับตัวอย่างข้อมูลทั้งหมดใน $S$ คราวนี้แทนที่เราจะคืน conjunction $h$ ออกไปเป็นคำตอบ เราจะพยายามตัด literal ออกจาก $h$ เพิ่มอีก ให้เหลือจำนวน literal น้อยที่สุดที่ยังคงสอดคล้องกับตัวอย่างข้อมูลทั้งหมดใน $S$

สังเกตว่าการตัด literal ออกจาก $h$ เพิ่มเติมนั้นไม่ได้ทำให้ความสอดคล้องของ positive example เปลี่ยนไป เนื่องจากสำหรับ positive example $a$ ใด ๆ conjunction $h$ เดิมนั้นต้องไม่มี literal ที่ขัดแย้งกับ $a$ อยู่ก่อนแล้ว และการตัด literal ออกจาก $h$ เพิ่มอีกไม่ทำให้มี literal ที่ขัดแย้งกับ $a$ ปรากฏขึ้นมาได้ อย่างไรก็ตาม หากพิจารณา negative example $a$ ใด ๆ การตัด literal ออกจาก $h$ นั้นอาจทำให้ไม่เหลือ literal ที่ขัดแย้งกับ $a$ อยู่เลย ซึ่งจะทำให้ได้ hypothesis ที่ไม่สอดคล้องกับ $a$ หากเราต้องการ hypothesis ที่สอดคล้องกับตัวอย่างข้อมูลทั้งหมด เราจึงต้องมั่นใจว่า literal ที่เหลืออยู่ทั้งหมดยังต้องสอดคล้องกับ negative example ทั้งหมดที่มีด้วย ซึ่งตรงนี้จะเห็นว่าเราสามารถมองปัญหานี้ในรูปของปัญหา Set Cover ได้ และใช้อัลกอริทึมด้านบนในการหาคำตอบที่รับประกันว่าจำนวน literal ที่เหลืออยู่จะไม่มากเกิน $size(c)\ln m$ เมื่อ $size(c)$ เป็นจำนวน literal ที่แท้จริงของ conjunction เป้าหมาย $c$ และ $m$ เป็นจำนวนตัวอย่างข้อมูลใน $S$

สำหรับแต่ละ literal $z$ ที่ปรากฏใน $h$ เราให้ $N_z\subseteq S$ เป็นเซตของ negative example $a$ ทั้งหมดที่ การมีอยู่ของ $z$ ใน hypothesis นั้นเพียงพอที่จะรับประกันความสอดคล้องกับ $a$ นั่นคือ $N_z$ เป็นเซตของ negative example $a$ ที่ $z=0$ ใน $a$ เราสามารถมองการเลือก literal $z$ ไว้ใน hypothesis ว่าเป็นการเลือกเซตที่ครอบคลุมสมาชิกใน $N_z$ ซึ่งจะเห็นว่าถ้าเรามีกลุ่มของ literal $z$ บางตัวใน $h$ ที่เซต $N_z$ ของ literal เหล่านี้ครอบคลุม negative example ทั้งหมดใน $S$ เราก็จะได้ว่า conjunction ที่สร้างจาก literal $z$ เหล่านี้จะเป็น conjunction ที่สอดคล้องกับ $S$ ด้วยเช่นกัน

ถึงตรงนี้จะเห็นว่าปัญหาการเลือก literal ใน $h$ ของเรากลายเป็นปัญหา set cover ซึ่งถ้าให้ $OPT$ แทนจำนวน literal ใน $h$ ที่น้อยที่สุดที่เพียงพอที่จะทำให้ negative example ทั้งหมดตอบ 0 ได้ถูกต้อง เราจะได้ว่า $size(c)\geq OPT$ ดังนั้น หากเราประยุกต์ใช้อัลกอริทึมแบบ greedy สำหรับปัญหา set cover เราก็จะรับประกันได้ว่า hypothesis $h’$ ที่เป็นคำตอบของอัลกอริทึมนี้จะเป็น conjunction ที่สอดคล้องกับ $S$ โดยมีจำนวน literal ไม่เกิน $OPT\ln m\leq size(c)\ln m$

การวิเคราะห์อัลกอริทึม

เนื่องจากจำนวน literal ของ $h’$ ที่เป็นคำตอบของอัลกอริทึมใหม่นี้จะไม่มีทางเกิน $size(c)\ln m$ เราอาจกล่าวได้อีกอย่างว่า เซต $H$ ของ hypothesis ทั้งหมดที่สร้างได้จากอัลกอริทึมใหม่ของเรานี้ จะเป็นเซตของ conjunction ที่มีจำนวน literal ไม่เกิน $size(c)\ln m$ เนื่องจากเรามี literal ที่เกี่ยวข้องทั้งหมด $2n$ ตัว ดังนั้นเราสามารถระบุถึง literal แต่ละตัวได้โดยใช้พื้นที่ $\log_2(2n)$ บิต หากเราต้องการระบุ hypothesis ที่มี literal ไม่เกิน $size(c)\ln m$ ตัว ก็จะใช้พื้นที่ไม่เกิน $size(c)\ln m \log_2(2n)$ บิต ดังนั้นจะได้ว่า

เมื่อนำขนาดของ hypothesis space นี้ไปใส่ในบทวิเคราะห์ของการเรียนรู้เมื่อ hypothesis space มีขนาดจำกัด เราจะได้ว่าสามารถเรียนรู้ปัญหา Boolean Conjunction นี้ได้โดยมี generalization error เป็น

หรือกล่าวได้อีกอย่างว่า อัลกอริทึมใหม่นี้ทำการเรียนรู้ตามกรอบการเรียนรู้แบบ PAC ได้เมื่อจำนวนตัวอย่างข้อมูลเป็นไปตามอสมการต่อไปนี้

สังเกตว่าอสมการด้านบนนี้ยังไม่สามารถบอก sample complexity ได้อย่างชัดเจน เนื่องจากด้านขวามือยังติด $\ln m$ อยู่ด้วย

การวิเคราะห์ sample complexity

ในการที่จะหาขอบเขตของจำนวนตัวอย่างข้อมูลที่ต้องการในกรณีนี้ สามารถทำได้โดยใช้เทคนิคในการหาขอบเขตของค่า $\ln m$ ดังนี้

พิจารณาฟังก์ชัน $y_1=\ln x$ และ $y_2=ax+b$ ที่ทั้งสองฟังก์ชันนี้มีค่าเท่ากันที่จุด $x=\alpha$ ดังรูป

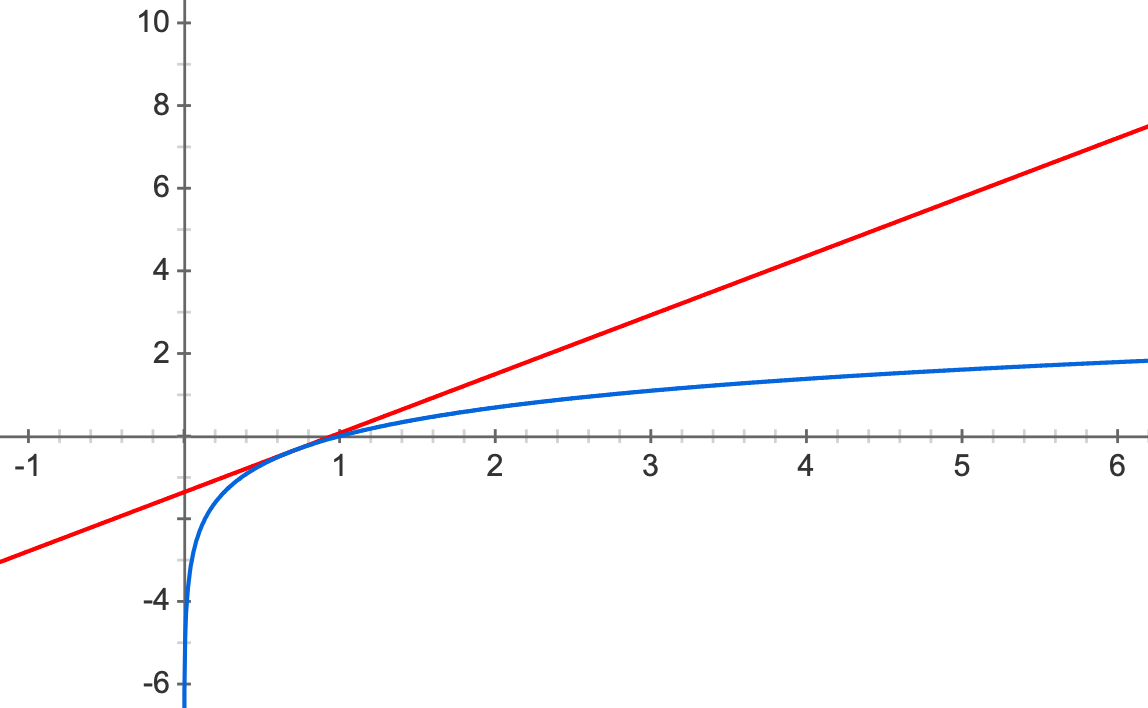
เนื่องจากที่จุด $x=\alpha$ ฟังก์ชันทั้งสองมีความชันเท่ากัน นั่นคือ

และที่จุดเดียวกันนี้ $y_1$ และ $y_2$ ก็มีค่าเท่ากัน นั่นคือ

หรือได้ว่า $b = \ln\alpha -1$ นั่นเอง

เนื่องจากฟังก์ชันเส้นตรง $y_2$ จะเป็นขอบเขตบนให้กับ $y_1$ เสมอ เราจึงสรุปได้ว่า สำหรับ $\alpha>0$ ใด ๆ

ดังนั้นเมื่อเราแทน $x$ ด้วย $m$ และแทนค่า $\alpha$ ด้วย $2size(c)\ln(2n)/\epsilon$ (ซึ่งมีค่ามากกว่า 0) เราจะได้ว่า

ถ้าเราพิจารณาค่า $m$ ที่น้อยที่สุดที่ต้องการในการเรียนรู้ กล่าวคือ ให้ $m=\frac{1}{\epsilon}\left(size(c)\ln m\ln(2n) +\ln\frac{1}{\delta}\right)$ เราจะได้ว่า

ดังนั้นเราจึงได้ว่า

หรือก็คือ

ดังนั้นเรานึงได้ว่า อัลกอริทึมใหม่นี้จะสามารถเรียนรู้ปัญหา Boolean Conjunction ตามกรอบของ PAC ได้ เมื่อมีจำนวนตัวอย่างข้อมูลอย่างน้อย $\frac{2}{\epsilon}\left(size(c)\ln(2n)\ln\frac{2size(c)\ln(2n)}{\epsilon} + \ln\frac{1}{\delta}\right)$ ซึ่งจะเห็นว่า อัตราการโตของ sample space นี้เกือบจะเป็นเชิงเส้นบน $size(c)$ โดยจะโตเป็น $O(size(c)\log size(c))$ ในขณะที่อัตราการโตเมื่อเทียบกับ $n$ เป็น $O(\log n\log\log n)$ หาก conjunction $c$ ที่ต้องการเรียนรู้นั้นมี $size(c)\ll n$ เราก็จะเห็นว่าอัลกอริทึมใหม่นี้มีประสิทธิภาพในการเรียนรู้ดีกว่าเดิม

Prev: Consistent Hypothesis

Next: การเรียนรู้ Boolean Conjunction ด้วย Inconsistent Hypothesis